三体問題について
この部分は「物理数学の直観的方法 第2版」11章の11−2の最後の部分(213ページあたり)につける予定だったもので、これまでの伝統的に三体問題に対してどういうやり方で数学者たちがアプローチを行なってきたのかについて、その要点を述べたものです。三体問題に特に関心のある読者以外には余計かもしれないと思って、とりあえず削除してしまいましたが、本で行なったやり方と比較すると面白いと思います。
(20001105 長沼伸一郎)
・三体問題への伝統的アプローチ
・二つのアプローチの比較
・本当にピリオドは打てないのか
・19世紀以降の三体問題
・残された大きな不満
§三体問題への伝統的アプローチ
ところでこの本では先ほど実にあっさりと三体問題の中枢部に手が届いてしまっていたが、実はこれは今回のアプローチがいわば正面玄関からの戦術勝負を避けて、一旦問題の外に出る格好で「そもそも方程式が解けるとはどういうことか」を問うという戦略勝負に全体を移行させ、その結果ほとんど無防備の裏口から進入できたことによる。
そう思って眺めると、18世紀以来の伝統的なアプローチの場合、それとは逆にそういう戦略的な迂回を行なわずに、まさしく防備の堅い正面玄関からまともに攻めかかり、ひたすら解析的な戦術面の高度化で遮二無二障害を突破しようとしたかの感がある。
一般に戦術だけに頼った正面攻撃というものは、大変な努力の割に滅多に決着がつかないのが普通なのだが、どうやらこの場合もまたその例に洩れなかったようである。実際これらのアプローチの多くは、おしなべて「卵の中から卵をゆでる」ような困難に直面せざるを得ない破目に陥ってしまい、三体問題の長い苦闘の歴史もある意味で納得が行く。
そこでその伝統的なアプローチがどういう思想で行なわれてきたかの要点を、ここで簡単に紹介しておこう。
さてまず三体問題への最初のアプローチは、これを「求積法」で何とかして解こうという考えで始まった。「求積法」などと言うと、何か非常に特殊な技法のようにも聞こえるが、何のことはない、要するに早い話、われわれが普通に代数演算、変数変換、積分操作などを用いて式をこねくり回して解を求めることをこう言っているに過ぎないのである。 なぜそれを「求積法」と呼ぶのかと言えば、恐らくこれを使って実際に問題を解く場合、いろいろと式変形を行なった後、最後に積分操作で仕上げをする形で問題にピリオドを打つパターンになることが多かったため、積分=面積を求める、ということで昔こういう名前がついて、その名残が今も残っているためである。
そしてその場合に基本となったアプローチは、「第一積分」(これまた古い妙なネーミングだが)という量をどうやって見出すかということであった。これは「保存量」とも呼ばれており、現在では天体力学以外の分野ではむしろ後者の呼び方の方がよく使われれるようだが、ではこれが一体どういうものかを簡単に説明してみよう。
例えばここにxとyを変数とするある方程式があったとして、これをいろいろ変形したところ、次のような式を一つ作れたとしよう。すなわちそれは、とにかく右辺が定数になっているような式ならどんなものでも良く、例えば今ここで思いつくままに考えた
exp(x+y)/xy=c
のような式でもよい。(そのためこの式の中身自体には特に意味はない。)
この式の場合、右辺を定数cとしてあるので、単にそれだけで先ほどの条件が立派に満たされることになり、こういう量がすなわち「保存量」なのである。
何だか話が簡単すぎてちょっと拍子抜けしてしまうが、とにかく右辺が定数である以上、当然式の左辺の値も常に一定、つまりこの式全体の値はどんな状況下でも一定値に保存されることになり、それゆえこの式のことを「保存量」と呼ぶことができるというわけである。
そしてこの量は三体問題では伝統的に「第一積分」と呼ばれてきており、とにかくこういう量を見つけさえすれば良いというのが、18世紀以来の三体問題の基本的なアプローチだったのである。(「第一積分」という妙な名前の由来も、恐らく先ほどの求積法のときの話と似たようなものだと考えれば理解できるだろう。要するに多分これらの量は、最初大体は右辺がゼロの式の形で求まっていたのであり、それを1回積分してこういう右辺が定数の形に直すことが多かったため「積分」の名がついたというわけである。)
さてそれでは、こういう量があると一体何ができるのだろうか。それを知るには次のようなことを考えればよい。
今ここで、外から何らかの形でxの値が例えば具体的にx=f(t)のように与えられたとしよう(fの中身は何でも良い)。この場合、当然ながらyは先ほどの式のxのところにfを代入して整理するだけで、例えばy=g(t)のような形に書き下すことができる。
さらに、変数がxとyだけでなくzも含んでいた場合には、この種の式(すなわち第一積分・保存量)がもう一個あれば、最初の式を使ってまずyを書き下した後に、続いてもう一つの式を用いて例えばz=h(t)のような形に書き下すことができるだろう。
そして変数の数がもっと多くなったとしても、式の数もそれに対応するだけの個数が存在していれば、それらすべてを次々に書き下していくことができることになる。
要するに以上をまとれば次のようになる。つまりある問題は、変数(あるいは自由度)の数だけこうした第一積分・保存量が存在しているならば、次々に変数の中身を書き下していける、つまり「解ける」ということになるというわけである。
実はこのあたりの話は、ある意味で一次方程式の話の拡張版と言えなくもない。それというのも一次方程式の場合、(当たり前のことだが)例えばx+3y+2z=5のような式を1個だけ与えられても問題は解けないが、同じような式があと2つあって、3つの式の連立方程式になっていればx、y、zの値が求まる。
つまりこの場合、変数3個に対して式が3つあれば良いというわけで、これは変数と式の個数の関係という点で先ほどの話と実に良く似ているが、実際両者は似ているというよりはむしろ実質的に同じ話なのである。なぜならよく考えてみると、先ほどの一次方程式のx+3y+2z=5のような式は、右辺が定数である以上、先ほどの定義に照らせばこれも一種の「保存量」であることには違いはない。
要するにそう考えれば、一次方程式の場合もやはり変数と同じ個数だけ「保存量」があれば解けるということになり、結局抽象的に見れば、話は全く同じことになってしまうのである。
さらにこの第一積分・保存量の場合、その記述にどの程度のツールが使われたかを見れば、解がどの程度のツールで記述できるかが自動的にわかるという、もう一つのメリットがある。つまり先ほどの例で言うと、yをy=g(t)のような形に書き下す作業は、第一積分の中で使われている関数の逆関数ぐらいまでを使えばできるはずだという話になるのである。
実際先ほどの例だと、この問題では第一積分は exp(x+y)/xy=c と表現されていて、もう一つ、x=f(t)という量があるに過ぎないのだから、それらを基に関係式をy= の形に書き直すには、せいぜい対数関数と乗法除法ぐらい(それとfの表現に使われている関数)を使えばできるということになるだろう。
そしてこの話に関しても、やはり一次方程式に置き換えて同じような話をすることができる。すなわち一次方程式の場合、各「保存量」(=連立方程式のそれぞれの一次式)は四則演算だけを使って表現されているので、解を書き下す作業も当然ながら四則演算だけを用いてできるということになるのである。
要するに以上をまとめれば、次のような結論になる。すなわち三体問題の場合、もしこの種の「第一積分」が、変数(ないし自由度)と同じ個数だけ存在し、なおかつそれら「第一積分」の表現が、初等関数とその導関数、および代数演算ぐらいを用いて可能であるということさえ示せれば、三体問題は求積法で解ける、つまり初等関数で表現できる解をもつことが証明されるというわけである。
まあ確かにこれは十分地に足がついた堅実な手法であり、恐らく当時の数学者たちの
目からすれば、このアプローチこそ三体問題の王道というべき攻略法に見えていたこと
は間違いなく、そのため彼らは早速皆で三体問題に関するこういう第一積分を探し始め
た。
そして18世紀にオイラーが「オイラー積分」の名で知られるものをいくつか見つけ
たが、いかんせんまだ個数が全然足りず、解が定まるどころの話ではない。そこで残り
のものをいかに見つけるかという課題が、これ以後の三体問題への伝統的なアプローチ
の基本となり、多くの数学者たちがそれに血道を上げることになったのである。
§二つのアプローチの比較
ところでこうした手法は、本書で以前行ったアプローチとは随分違っているようにも見えるが、では両者は本当に関連をもっているのだろうか。それを次に見てみよう。
まず今の話が、表現形式こそ違え、背後で行列の概念と何らかの形で関係があるらしいことは推察できる。
それというのも先ほど第一積分の概念を説明するときに、それを「連立一次方程式の拡大版」というイメージで捉えたが、考えてみれば連立一次方程式とはすなわち線形代数のことなのだから、線形代数の延長である作用マトリックスとこれが関係してくるのは、むしろ当然だろう。
ではそれをもう少し具体的に見てみるとどうなるだろう。例えば先ほど述べた話では、第一積分の個数が十分にあれば問題が解ける、すなわちまず最初にxがf(t)のように与えられていればそれを用いて、続いてy=g(t)、z=h(t)という具合に次々と解を書き下していけるということだった。そしてこの話は、連立一次方程式のアナロジーで考えるともっとクリヤーに捉えることができる。
すなわち連立一次方程式の場合(これは読者も経験があるだろうが)、式をきれいにするため邪魔な項をどんどん消去していって、ついに解を一挙に書き下せる直前の段階に達したとき、式全体は大抵は次のような形になっているものである。すなわちそれは、例えばまずxだけはすでに
x=a
という形で値が求まっており、そして続いて残りの式が
2x+y=b,
x+3y+2z=c,
・
・
・
というようにピラミッド状に整理されている状態である。こうなっておりさえすれば、もう後は次から次へと結果を下に代入してx,y,z,・・の値をすべて書き下していけるわけである。
そしてこの状態は線形代数による表現も可能であり、その場合には今の式全体が
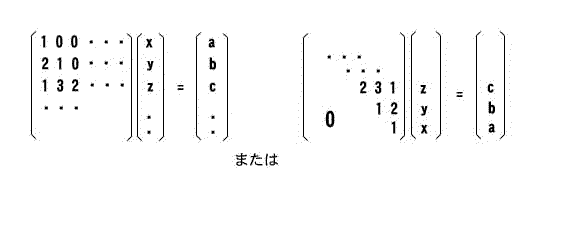
という形に表現されることになる。そしてこの場合言うまでもなく、右辺の列ベクトルの中のa,b,c,・・・の値がちゃんと全部(つまり変数の個数と同じだけ)与えられていることが、解を一挙に書き下せるための条件である。
そしてこの話はそっくりそのまま第一積分の話にも置き換えることができ、そしてその場合、右辺の列ベクトルの中の数値a,b,c,・・・などの部分を、たくさんの第一積分で置き換えてやればよいわけである。(そして無論その個数が足りているか否かが「解ける」ための条件である。)
しかしそんなことより大事なのはこの行列の形そのものである。つまりこれは一見してわかるように上三角行列の形になっている、つまりまさしく本の210ページと同じことになってしまっているのである。
これを見る限りでは、第一積分方式と作用マトリックス方式は明らかに同じ課題に対する異なる表現形式であるということが推察されるであろう。(ただし両者は全く同じかというとそうとも言えず、第一積分方式の場合、その中には本で述べた議論の残りの部分、すなわち「解の記述が可算無限の手間でできるか」という話が基本的に欠けているようにも見受けられる。ただしそれについては後ほどもう少し詳しく論じる。)
両者の比較(1)・それぞれの長所と短所
では両者のアプローチを優劣の面から比較した場合、それぞれの長所や短所はどのようなものになっているのだろうか。それを次に見てみよう。
まず第一積分・保存量方式の長所について言うと、こちらの場合先ほど述べたように、第一積分が全部見つかって「解ける」ことがわかった時点で、自動的に解がどの程度の関数や数学的手段で記述できるかもわかってしまうというのが、大きなメリットである。(それに対して作用マトリックス方式だと、たとえ対角化可能だということがわかっても、解がどの程度のものになるかはすぐにはわからない。)
一方逆に第一積分方式の弱点について言うと、たとえ第一積分があれば解を書き下せるとは言っても、やや辛辣な言い方をするならば、それは単に問題を左辺から右辺に移しただけのことではないかとも言えなくもないのである。
実際それはその通りなのであってこの場合、今度はその肝心の第一積分を一体全体どこからどうやって見つけてくるかという問題が新たな難問として立ち塞がってしまい、やはりすぐに前進不能になってしまう。要するにこの場合、問題の難しかった部分がほとんどまるごと左辺から右辺に引っ越しているに等しく、問題の難しさ自体は結局大して軽減されていないのである。
実際、三体問題と格闘した過去の数学者たちも、ほとんどがここで泥沼に足をとられて一歩も進めなくなっていたのだが、こうしてみるとまあそれは当然と言えば当然のことであろう。要するにこれは式を一段階きれいにしただけのものに過ぎないわけだから、この程度のツールを唯一の切り札として前進せよと言われても、困惑するのが当たり前だったのである。
両者の比較(2)・「解けない」ことはどうやって断言するか
それともう一つ、第一積分方式の弱点について言うと、この方式ではたとえ「解けない」ことが一応証明されたとしても、本当にそれで話が終わったと断言できるかどうかがかなり怪しいという宿命的な弱点がある。
例えば三体問題の場合、19世紀の終わりまでには普通の関数(解析的な概念による)の枠内では、一般には第一積分の個数が不足してしまうことが示されており(それは逆に言えば、恐らく簡単に式をきれいにできる部分だけが第一積分として現われているということなのだろうが)、少なくともそのレベルでは三体問題は「解析的に解けない」ことが示されている。
しかしそれではもっと想像力を広げて、遠い将来に何かわれわれが未だ知らない、普通の「解析的な関数」を超える概念が出現してそれによって天体の運航を記述できるようになり、そういう形で「三体問題が解かれる」ことも絶対にないと断言できるのかと言われると、この方式ではそれに答えるのは基本的に難しい。つまりその意味で、話に本当にピリオドを打つことができないわけである。
実はこれは先ほどこの方式のメリットとして挙げたこと、すなわち「右辺の第一積分の性質がわかっていれば、自動的に解の性質もわかる」ということが逆に弱点となって生じている問題なのである。
もう少し詳しく言うとこの方式の場合、そのメリットゆえ右辺の第一積分の性質として例えば「解析関数」という条件を考えれば、左辺についても「解析関数の範囲で」解けるか否かがわかるし、あるいは右辺を一次式の範囲に設定した場合には、一次式の範囲で解けるか否かがそれぞれわかる。要するにこの場合、右辺の条件をどう設定するかに問題全体が完全に支配されているわけである。
ところがそれはそっくりそのままこの方式の弱点でもある。それというのもこの方式の場合、(先ほども述べたように)右辺が設定できれば左辺もわかるということを言っているだけで、肝心の第一積分をどこからどうやって見つけて来るかという問題に関しては、何も手段を提供していない。
つまりもしその一番大事な作業の部分を、「われわれの知っている関数」の概念を想定してその体系の中で進めてしまうと(現実問題、この場合そうする以外に手がない)、結論もやはりその枠の中から出ることが基本的に出来ないのであり、その外のことには完全に無力である。
そのため三体問題の場合も、右辺の第一積分が存在しないことがわかれば一応解けないことがわかるとは言うものの、真の意味で三体問題のピリオドとなる質問、すなわち「この世には三体以上の天体の運航を数学的に解き明かす一般的方法は、(未知のものも含めて)絶対に存在しないと断言できるのか」を問われると、それは言えるようにも言えないようにも見えてだんだん頭の中がこんがらがってきてしまい、結局議論に真のピリオドを打つことができないのである。
まあそれはこの「可積分系」という方式の本質的な限界であって、もともとこの方式は「解ける」を言うときに最高の能力を発揮するよう設計されており、「解けない」ことのピリオドを打つには必ずしもベストの道具ではないと言えるだろう。
§本当にピリオドは打てないのか
しかしそれならば、この「最後のピリオドを打てない」ことを人類の知性の限界として諦めてしまうべきかと言えば、どうも必ずしもそうとは言えないようである。それというのも作用マトリックスN乗方式を使うと、ある意味でここのところはクリヤーに言うことができるからである。
つまりこの場合、問題の本質を「解の情報の記述が可算無限個の手間でできるか」という一点から捉え直し、そこから評価を一元化していけばよい。
実際、もし仮に如何なる手段を用いても、ある問題に関する一般的な解の情報の記述が可算無限個の手間ではできないとすれば、それは即ち人類が動員できる如何なる方法によっても物理的にそれが不可能であることに他ならないからである。
そしてさらに完璧を期すとすれば、ここで「初期条件などの入れ替え作業をそこから分離できない」という話も示されていることが望ましい。
どういうことかと言えば、たとえ厄介で膨大な非可算回の手間を要する部分が現われてくるのを避けられないとしても、もしそのシークエンスが常に共通で、そこだけを本体から分離できるとすれば、実質的には何も問題はないわけである。
実際その場合は、そういう厄介な部分は一まとめにして何か記号のラベルでも貼っておき、初期条件の変更に際してはそれにかかわる部分だけを分離していじれるわけだから、ある意味で系の振る舞いは一般的な数学的表現がなされていると言って良い。
そしてそういうことができないことを証明するのは、作用マトリックスを使えば容易であり、そして最終的にそれらすべてが出来ないとすれば、あらゆる初期条件についていちいち非可算無限の手間が必要になるわけで、これは人類の使えるいかなる手段によってもそれを解く「一般的方法」がないことを意味するわけである。
注) なお、今と同じ話をどうしても第一積分方式を用いた体系の用語を使ってその中で行ないたいのであれば、一応それは不可能ではない。
つまりその場合には、要するに問題を逆に左辺から右辺にそっくり移してしまえばよいのであり、「右辺の第一積分の記述自体が可算無限個の手間で可能か否か」ということを新たに問題にしていけばよいことになる。(ただしその場合、それを調べる作業にどのみち作用マトリックスが必要になってしまい、あまり意味のない余計な寄り道になってしまう可能性が高いのだが。)
両者の比較(3)・宇宙に「解ける」方程式は一体いくつあるのか
もう一つ、さらに無いものねだりをすれば、第一積分を探す「可積分系」の体系の中にいると、三体問題とハーモニック・コスモス信仰の関係が、過去300年間の数学者たちの死闘の歴史の上にどの程度影を落していたのかが見えにくい。
一方その割にはこの体系の中には(三体問題に関する限りさほど役に立たない)戦術的な小道具だけはやたらにたくさんあってそれに幻惑されがちであり、そのためこの体系の中に身を沈めていると、もっと単純で基本的なことの重要性をきれいに忘れてしまう危険が大きいのである。
実際そのあたりが、本来この三体問題が思想や文明の上に巨大なインパクトを秘めているはずであったにもかかわらず、それが長いこと気づかれずにきてしまった大きな原因の一つであったようである。
それはともかく、ひとたびその盲点が明らかになるや、作用マトリックスN乗の思想は慄然とするほどの切れ味を見せ始める。
例えば次に示すような一見人間には手の届きそうにない問い、すなわち「一体この世界に存在するすべての微分方程式のうち、解けるものはどのぐらいあるのか」などという途方もない問題に対しても、これを用いると極めてクリヤーな結果が得られることになる。
こんなことはちょっと見る限りでは、到底人間の想像力を超えたもののようにも思えるが、しかしそれは意外に単純なことなのである。ここで、本の三体問題のところで述べた次の基本的な原理を思い出してみよう。すなわち
・一般に微分方程式を作用マトリックス形式に書き直した場合、もしそれが対角化できるならばその方程式は「解ける」し、対角化不可能ならばその方程式は「解けない」。
ということだったが、これを用いると先ほどの問題は次のように書き換えることができる。すなわち
・この世界にあるすべての作用マトリックスを考えたとき、もしその中に対角化できるものがいくつあるかを知ることができたとすれば、それはすなわち「この宇宙にある微分方程式のうち解けるものがいくつあるか」の答えと同等である。
ということである。
さて、問題をこのように言い替えたは良いが、一見すると今度は「対角化できるものがいくつあるか」ということが新たな難問となって、大して先へは進めないようにも思える。ところがまさにここが盲点なのである。
ここでちょっと原点に立ち返って、「対角化」ということをあらためて式に書いてみよう。すなわちある行列(作用マトリックス)Aは、適当な変換行列Pを用いて
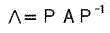
という具合に対角化されるわけだが、ここで逆に式をAについて書き直してみよう。すなわちその場合当然
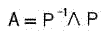
ということになる。
一見するとただ右と左を入れ替えただけのようにも思えるが、実はこの式は集合という観点から見た場合、思いも寄らず重要なことを言っているのである。
すなわちこの場合、まず左辺のAは当然ながら「解ける」方程式全体の集合に相当しており、また右辺の対角行列Λは解の関数全体の集合に相当している。
ところがこの式全体を眺めると、その左辺のAがPとΛの組合せで表現されてしまっているという事実にあらためて気がつく。
つまりそれは、左辺の集合Aは、実は右辺にある対角行列Λの集合をベースにして、それを変換行列Pを使って膨らませて作った集合なのだと解釈することも可能だということである。そしてさらに一歩進めて言えば、要するに集合としてのAは、集合Λと集合Pの直積集合だと考えて事実上差し支えないことになる。
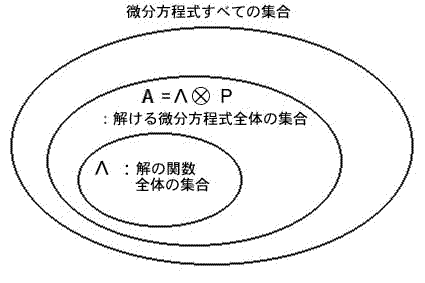
そうなると、当然ながら集合Aの中身が一体何個あるかの上限もまた、ΛとPの直積集合を超えることはない、つまり
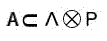
ということになるのだが、ここで重要なのはこの場合、右辺のΛやPの集合の中身がそれぞれいくつあるかは基本的にわかる(ないし設定できる)ということである。
例えば一般に対角行列の集合Λを考えた場合、それが普通の行列全体の中ではどの程度のサイズの部分集合になるかを知るのはそんなに難しいことではない。実際極端な話、例えば行列のサイズを5行5列と決めて成分の内容を整数に限ってしまえば、それがいくつあるかの割合は具体的な数値として示せるし、分割を無限小にして連続化した場合でも、抽象的な集合としてならその割合を求めることができる。
そしてそれは変換行列Pに関しても基本的には同様であり、そのようにして集合Λと集合Pのサイズがわかるとなれば、結局それらの直積集合のサイズもわかってしまうことになり、最終的に集合Aのサイズの上限がそれで決まってしまうのである。
そして以上の議論をまとめて、あらためてその意味を言葉にすれば、それがすなわち先ほどの問いへの答えとなる。
つまり「宇宙にあるあらゆる微分方程式のうち解けるものが一体いくつあるのか」と問われたならば、集合Aのサイズおよびその全体に対する比率が、それへの解答を意味するというわけである。(なおこれは三体問題の場合で言うと、問題全体の中で制限三体問題などの形で「解ける」ケースがいくつあるかという問題に対応している。)
しかしその結果は衝撃的である。実際これを見る限りでは、どうやら方程式全体の中では、解けるもの割合はどう見てもほとんど無限小(解析学の用語では「測度ゼロ」)に近いのであり、その真相たるや「解けるものは非常に少ない」などという生易しい表現で追いつくような代物ではなかったのである。
(ただし以上は多少単純化されているので、完璧な証明にするためにはもう少し小手先の技術的な修正が必要である。しかしながら問題の本質自体は、以上で言い尽くされており、結局はこの結論に帰ってくることになる。)
それにしてもこんなに重要なことがこんなに単純に明らかにできるというのは、ある意味で驚くべきことであり、第一積分を用いる在来型の手法を用いている限りは、こうしたことは盲点に入り込んでしまって、まず見えてはこないものである。まあそのこと自体、如何に数学者の頭脳が長きにわたってハーモニック・コスモス信仰の呪縛の中にあったかの証拠なのだが。
§19世紀以降の三体問題
さてそれでは話を元へ戻して、三体問題の進展はその後は一体どうなったかというと、その中心課題であった「第一積分探し」に関しては、大勢の数学者が血眼になって探し回ったものの、結局オイラーが見つけたもの以外のものはさっぱり見つからずにそこから先は事実上打ち止めになってしまい、問題は完全な膠着状態に陥った。
その一方で、実用上必要になる天体力学の軌道計算については、いわゆる「摂動法」による近似によって、とにかく膨大な手間をかけて少しずつ軌道の修正を続けていけば数値そのものは求まることがわかり、解を求めることの死活的重要性はとりあえず軽減されていった。
そこでむしろ、数学者たちの関心はそれが解けないことを証明することの方に向かうことになる。そしてそのためには先ほどとは逆に第一積分が存在しないことを示す、つまり、もしオイラー時代までに見つかっているもの以外の、(独立した)第一積分が存在したと仮定すると式の中に矛盾が出ることをどうにかして示せばよいわけである。
もっともそうは言っても、何しろこれは「卵の中から卵をゆでる」ようなものであり、尋常のことで出来るものではないが、しかしとにかくメカニズムの本質がどうなっているかはこのさい問題にする必要はなく、矛盾を一例こね上げることができればそれで良いということだったので、とりあえずそれでも何とかやりようはあったわけである。
まあこれは今から見ると、局面が袋小路に入り込んでいるのに戦略面での抜本的な見直しを行なわず、そのかわり小手先の戦術だけをひたすら高度化することで乗り切ろうとしたに等しいのだが、ともあれそういう戦術的アクロバットの末、19世紀の終わりごろまでにブルンスやポアンカレなどの数学者によって、少なくともわれわれが普通に考える「関数」の形ではそういうものが存在しないことが証明され、求積法などの伝統的な数学的手段でそれを「解析的に解く」試みには一応の終止符が打たれた。(この部分の具体的な詳細については、例えば大貫義郎・吉田春夫著「岩波講座 現代の物理学1・力学」などを参照すると良い。)
§残された大きな不満
しかしこれは多くの人にとって、「終止符」と呼ぶにはあまりにもすっきりしない、不満の残るものだったようである。その理由は(先ほど述べた弱点も含めて)いろいろあるだろうが、しかし何と言っても最大の理由は、これらがあまりに技術的になってしまって見通しが悪すぎ、三体問題が人類の前に立ち現れてきた時に抱かれた根源的な問い、すなわち「これほど単純で本質的な問題が解けないというならば、その根本的な理由は何なのか」を直観的に知りたいという切実な要求に、ほとんど答えられなかったことによることが大きいようである。
またポアンカレの仕事の場合、とにかく複雑な戦術的アクロバットの組合せで無理矢理結論にたどり着いたという感じが強く、およそ「素直に本質を捉えた広く一般に使える手法」という感触からはほど遠い。
(ところで余談だが、どうもポアンカレという人は、数学業界からの評価はともかく、物理屋に採点させるとその評価ががくんと下がるという傾向があるらしく、技術的な冴えは超一流だが思想的な本質を捉える能力がやや甘い、要するに天才ではない大秀才、というあたりが、物理屋くさい物理屋からの一般的な評のようである。)
実際、結論に汎用性が乏しくて他の分野への広い応用がほとんど効かないというのは、彼らの行なった仕事の大きな弱点の一つである。そしてその観点から一般に過去の他の数学の問題の例を振り返ってみると、そこに真の意味での終止符が打たれた時には、その瞬間に一挙に視野が開けて、類似の問題が全部まとめて射程内に入ってしまうことが多かった。
一方逆にそういうことが起こらない間は、たとえ散発的にいくつかの結果が出てきて一見決着がついたように見えても、大抵の場合それらは後になって単なる特例の一つに過ぎないことが判明して評価が格下げされ、結局真の終止符は後に登場するもっと根本的な体系の登場まで持ち越されるという場合がほとんどだったのである。
まあ三体問題の場合、とにかくこれまで他に使えるツールがなかったため、19世紀の体系やその評価をそのままにしておかざるを得なかったわけだが、少なくともその条件に照らしてあらためて振り返って見る限り、どうもポアンカレの仕事はそれをクリアしているとは言い難い。
それゆえ、数学者の中には彼の仕事が三体問題の終止符だったという人もいるにはいるのだが、将来においてこの問題全体の大規模な再検討が行なわれる可能性が高く(何しろ従来の主力だった「可積分系」で扱える問題の個数が実は何と最初から「測度ゼロ」だったのである)、そしてその際にはこれらの評価も現在とは大きく変わってくることが十分あり得ることを考えると、ここは一応それについて懐疑的な態度でいたほうが賢明であろう。

