三体問題と『部分と全体』の300年 第1回
Update: 2009/04/15
・この記事は、理系への数学 2009年 04月号(現代数学社)に掲載されたものです。
昨年度に本誌4月号から12月号まで「ベクトル解析と理系世界の20年」というタイトルで行った連載は、お蔭様でご好評をいただいたが、その9回だけではどうも多くのことを書ききれなかったように思われる。そのため今号からいわばその第二部という形で連載を再開し、タイトルも新たに「三体問題と『部分と全体』の300年」という形に改めて、その話の続きをしていきたいと思う。
では新しくお読みいただく読者のために、前年度の連載を振り返りつつ、新しいタイトルをなぜそうしたかの理由などについても述べていこう。
昨年の連載は当初は、筆者が「物理数学の直観的方法」を出版して20年になり、その中で最も反響のあった第5章「ベクトルのrotと電磁波」の内容に関して、加筆をしつつ再度論じていくということから始まったものだった。しかしその20年の間に何だか理系世界を巡る状況自体がひどく悪化しており、若い世代の周囲の光景を見ても、例えば街を歩いている女の子に「世の中で最も頭のいい人は誰ですか」と聞いたとき、その答えの筆頭がお笑い芸人で理系がその下に置かれるなどということは、当時26歳だった筆者の周囲にはさすがに無かったように思われる。これでは若者の理系離れも無理もなく、そのため毎回の連載の後半部分で「理系世界の20年」という形で、どうして理系がここまで敬意を払われなくなったかについて思うところを述べていったわけである。
振り返ってみると、例えば筆者も高校時代には、高度に専門主義化された人間を集めた理系側は数を集めれば集めるほど力を増すのだから、同じような広く浅い知識しか有さない文系側に結局は全ての点で優位に立ち、最終的にはその使われ人になることなど理屈から言ってあり得ないと信じていた。にもかかわらず現実はなぜ逆なのだろうか(昨年度6月号)。
もっとも過去を見ると全ての場合にそうだったわけではなく、大体なぜか日本の理系は「海」というものと結びついた時に社会的に力を得ているのだが、ここで近代日本の理系集団の出発点だった幕末の長崎海軍伝習所を眺めると興味深いことがわかり、そこでオランダ人教官たちが「海軍の頭脳はゼネラリストでなければ用をなさない」つまり細分化された専門家をいくら集めても駄目だという重要な指摘を行なっていたのである(7月号)。
これは先ほどの理屈とは真っ向から矛盾するのだが、現実には確かに彼らの言う通りだったのであり、筆者はその奇妙さに悩んだのだが、それを考えるうちに、この問題が一つの問題に焦点を結んでいるということにだんだんと導かれていった。それがタイトルにもある「部分と全体」の失敗ということである。
どういうことかというと、理系世界の人間は一つのことを叩き込まれて育つ。それは一般に物事は部品や部分に細分化し、それらを精密に分析して最後に全部をつなげることで、それまでの文系の常識では到底できなかった高度なことがわかるということであり、300年前に始まったこのいわゆる要素還元主義こそが、科学の勝利の原動力だったわけである。
しかしこれが成り立つためには、一つの原理が成り立っていることが大前提で、それは「部分の総和が基本的には全体に一致する」ということである。実際これが成り立っていなければ、せっかくパーツに分けてそれぞれを精密に分析しても、最後に合計した時に値が別物になってしまうというのでは、方法論の全てが根底から覆ってしまうことになる。
ところがどうやらこの前提に根本的な問題があり、近年になって理系への敬意が崩壊したことの根底にはこの重大な問題が横たわっているように思えてならない。そしてその最大の鍵を握っているのが、実は「三体問題」なのであり、人類がここをよくわからないままバイパスしてきたことが、後の思想史や人類史のコース全体を大きく変えてしまったのではないかと考えられるのである。
さてその三体問題だが、読者もご存知のように一般に天体の個数が2個までなら問題は完全に解けるが、それが太陽、地球、月のように3つになると途端にその方程式は解けなくなり、いまだにその解は見つかっていない。それがなぜ解けないかについては300年の間いろいろな物理学者、数学者が論文を書いてきたが、その理由を直観的に理解するとなると難しい。
ところがここでその数学と哲学の狭間に生じる部分を、一種コロンブスの卵的な「作用マトリックスN乗」というツールを用いると直観的に明確に示すことができるのであり、それによって筆者自身、高校時代から抱えていたそれらの疑問にまとめて決着をつけることができたのである(昨年度9月号)。
そのツールに関する復習は次号でもあらためて行なう予定であるので、ここでは外見だけを簡単におさらいしておこう。(そのため今月号からお読みになる方は、昨年度9月号あるいは「物理数学の直観的方法」の第11章「三体問題と複雑系の直観的方法」をご参照いただきたい。)
そのアイデアの基本を一言で言えば、多数の天体や職業集団(あるいは人体ならば各器官)などで構成される系があったとき、それらの間の相互作用だけを一個の独立した行列にまとめてしまい、それを列ベクトルに何回もかけることで「動き」を表現しようというものである。
具体的に言うと、まず各天体間などの相互作用を残らず書き出してそれを縦横に並べて、一種の演算子を成分とする行列を作る。一方天体の位置情報などは列ベクトルの形で縦一列にまとめ、先ほどの行列をその列ベクトルに左から1回かけると、新しい列ベクトルには各天体の1秒後の位置が示される、という格好にしてやるのである。
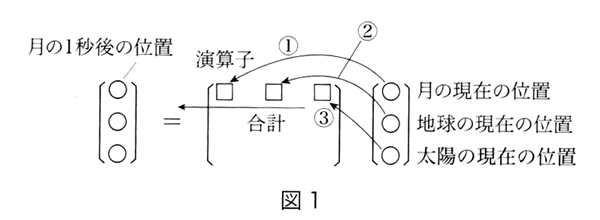
つまりこれをN回繰り返せばN秒後の天体系の状態が示されるわけで、基本的にこのような形で系全体の「動き」を記述できることになる。そしてこれは社会や人体などの系に関しても同様で、常識で考えられるどんな系でも原理的にはこのような形で表現できるはずである。そこでこの行列のことを「作用マトリックス」と呼ぶことにしよう。
もっとも別にこのような形式に書いたからといって、今まで解けなかった難しい問題が解けるようになるわけでは全然ないのだが、ここで一つ発想の転換を行ない、これを何か問題を解くためのツールではなく、むしろデカルト以来の「部分の総和が全体と一致するか」という哲学的な問いに数学からアプローチするためのツールとして用いようというのである。
つまりこの場合「行列を分割した形でN乗計算ができるか」ということに注目するとその鍵が得られるのであり、具体的に言うとこの場合、列ベクトルや行列内部を専門分野(経済や軍事など)ごとのカテゴリー別にいくつかに分割し、それらを別個にN乗して値を求めることが「問題を専門分野に分けて分析する」ことに相当する。そして最後にそれを寄せ集めた値が、もし全体を分割せずにまるごとN乗した結果と一致するというなら、それは「問題を専門分野や要素に細分化して扱える」ことを意味すると解釈して良いということである。
ところがここで、行列演算の基本法則が意外な盲点を明るみにするのであり、それは実は、そのような形で行列内部をいくつかの小行列に分割して、各個のN乗の結果を単純にその位置にはめ込んだものは、一般の場合には全体をN乗したものとは一致せず、それが一致するのは、次の図のように小行列以外の部分がゼロであった場合のみだということである。
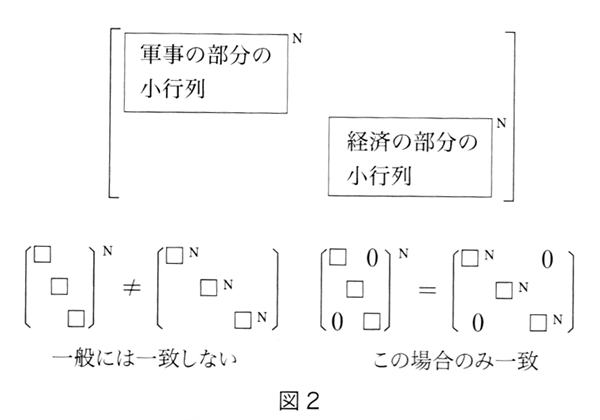
これは一見すると数学的には非常に単純だが、その哲学的な意味は想像もできないほど大きい。まず第一は先ほど述べたように、およそ考えうるいかなる系でも原理的には一応この形式で記述できるはずだということであり、そして第二に、この演算法則は非常に基礎的なものであるため、逆に言えばこの上にあるどんな複雑高度な問題も結局はそこから逃れることができないことである。つまりもしデカルト主義の本質がこのような形に置き換えて表現されるなら、実はこれはまさに「一般には部分の総和は全体に一致しない」という哲学的命題が数学的に示されることに他ならないのである。
そしてここから逆説的に浮かび上がってくるのは、近代における「デカルト的合理主義の暴走」の本質が、どうやら先ほどの相互作用成分を勝手にゼロと置いてしまったことにあるらしいということである。そしてここで、天体力学が最初に成功を収めた場所が太陽系だったことが重大な意味をもってくるのであり、実はそれはたまたま二体問題に分解できる特殊なケースだったのである。
つまり具体的に言うと太陽系の場合、各惑星同士の重力相互作用は非常に弱いので、そこを近似的にゼロと見なすことができ、それは作用マトリックスで書くと、図のような形でゼロ成分が入り込む形になっている。ところが実はこのパターンは、各惑星ごとに太陽との間で2行2列の小行列を作ってそれぞれを別個にN乗することができ、その結果を最後に集めれば全体をN乗したものと一致してしまうという、一種の特殊パターンなのである。
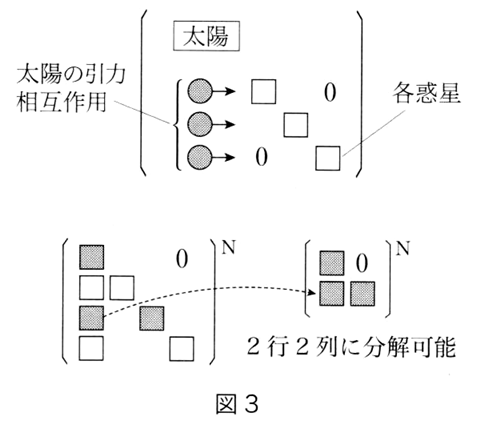
ところが人類が解析学を最初に適用して大成功した場所がその太陽系だったことが、巨大な錯覚を生み、そこでの天体力学の目も眩むような成功体験が、相互作用成分を勝手にゼロと置くアプローチを無制限に拡大させていき、それは世界そのものが基本的に「調和的宇宙=ハーモニック・コスモス」なのだという信仰に発展して、結局「物事を各個の部分に分割して解析できる=部分の総和が全体に一致する」という錯覚を哲学の根本部分に侵入させたのではないか、というのが昨年の連載内容の大筋である。
逆に言えばもし300年前に、三体問題の本質がこのようなツールでもう少し詳しく検討されていれば、その錯覚は生まれなかった可能性があるのだが、そう考えると人類がそこをバイパスしてしまったことが世界史のコースそのものに影響を与えたとも言えるだろう。これは決して誇張ではなく、まさにそれが劇的な形で爆発してしまったものこそ、現在われわれが目にしている「百年に一度」と言われるこの米国発の巨大経済危機ではないかとも考えられるのである。そこで、時事問題として極めてタイムリーなので、本来の話題だった三体問題などに関しては次号以降に述べるとして、初回である今回はとりあえずこれについて述べることとしよう。
現在の金融危機と天体力学
それにしてもこうして考えてみると、天体力学というものが世界史に与えた影響の大きさにはあらためて驚かざるを得ないのであり、そもそも米国流の自由主義というものも、天体力学が存在しなければ成立し得なかったのではないかと思えるのである。実際にその社会思想の発展史をたどると、それは全てジョン・ロックから発しているのだが、そのジョン・ロックは要するニュートンの天体力学を社会に適用することを行なったのであり、そう考えれば影響の大きさがわかろうというものである。
それはともかく、天体力学が米国の自由主義に与えた影響は2点があったと言えるだろう。まずその一つは「自由放任の神の手」による予定調和への信仰で、それというのも太陽系を眺めれば一目でわかるように、放っておいても各惑星は安定した円もしくは楕円軌道を周回し、その角速度や距離などは一定の幅で増減しながら大きな秩序を作っており、それが数十億年の間繰り返されている。
つまりこれを社会に適用すると「物事は放っておけば自然に一番安定した秩序を作る」という自由放任思想になるわけで、それまで人類文明には存在しなかったこの思想の誕生に、イメージ面でこれ以上大きな影響を与えたものは無かったのではあるまいか。
そしてもう一つは、「個人は各自が願うものだけを求めて自由に行動する権利がある」という信念で、これにも「世界が根本的には太陽系型である」という天体力学のビジョンが大きく影響しているように思われる。つまり太陽系においては各惑星の動きは互いに独立に扱うことができ、どれか一つの軌道を多少変更しても(三体問題と違って)全体への影響はほとんど無視できる。その意味では各惑星は自由な軌道変更を選択する権利を有していると言えるわけで、このイメージが「社会を構成する一人一人の個人はすべて自分の思うままに従って独立かつ自由に行動する権利がある」という考えに決定的な影響を与えたと思われるのである。
ともあれもし、世界や宇宙が基本的に太陽系型であるという「調和的宇宙=ハーモニック・コスモス信仰」が正しいとすれば、個人絶対主義も市場万能主義も最も宇宙の摂理に適ったことだということになり、その障害となるものは基本的に悪としてこの世界から取り除いていくべきだということになるだろう。いわゆる「規制緩和」などはその一環で、彼らにはそれを阻害する様々な規制などは社会の敵としか見えていなかったに違いない。こう考えると、米国人たちのちょっと理解しがたいほどの自由主義・個人主義への思想的こだわりも納得が行くのであり、実際に彼らは建国以来二百年以上にわたって、ある意味真面目にそれに邁進してきたわけである。
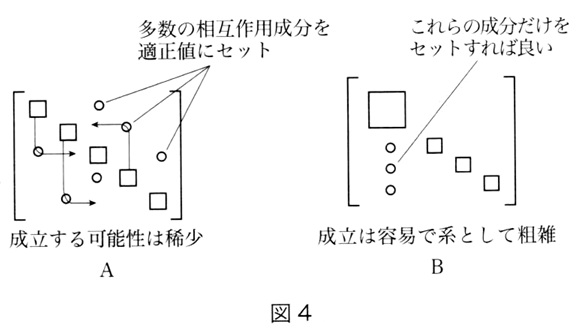
それは言葉を換えれば、無意識のうちに社会を太陽系型に改造しようとしてきたということであるが、しかし健全な社会状態とは、図のAのように社会の各部に相互依存の糸が緊密に張り巡らされた状態なのであり、一方経済社会をBのように太陽系型に近づけていくことは、要するにそれらの糸をどんどん切ってその経路を単純化していくことに他ならない。
そのためこれを推進していくと次のようなことが起こる。例えば商店街の壊滅などはその好例で、昔は町の経済は商店街が担って地域社会と二人三脚の形で街を支えていたのだが、現在では多くの場合、都心の巨大店舗がその経済機能をまるごと奪い取る形で商店街を壊滅に追い込んでいる。このとき全体が都心の大企業と住宅地の消費者という直線的な関係に変わっているが、これは作用マトリックスで書いてみれば、まさに太陽系型への変貌であることがわかるだろう。
もっともこの場合、確かに地域社会は壊れているが、その一方で大企業の側は空前の売り上げを達成して数字の上では経済活動全体は活気づいているため、結局はその良し悪しは相対的だとの理屈も一見成り立つように見える。しかし作用マトリックスを使うと、実はこのとき変化の前と後で系全体が一段階劣化していることを数学的に示すことができるのである。つまり前者は一種のデリケートな生態系に似ていて、作用マトリックスの多数の相互作用成分を全部、Aのようにバランス良く適正値にセットしなければ成立しないのに対し、Bの太陽系型なら太陽から各惑星への各一個づつの相互作用成分だけを適正値にセットすればよいわけで、偶然にそれらの系が成立する可能性は前者の方が希少である。それはもう一歩進めれば、この変化が客観的に見てもエントロピー増大を伴っているという理屈になり、こういう現象をここでは「縮退」と呼んでいる。
大体においてサービス業の隆盛というのは家族の崩壊と二人三脚で進んでいることが多いことなど見ると、どうやら一般に「社会を縮退させるとその過程で儲けが生まれる」ということが言えるように思われる。つまり資本主義は無から豊かさを生み出していたわけではなく、実は社会を縮退させてそこからエネルギーを搾り出していたのだということになり、まずここに大きな錯覚があったのである。
そしてこの問題にはもう一つ大きな錯覚があり、それは、そのようにして縮退が始まると、もはや安定的な復元が起こらず、そうやって育った大勢力が一方通行的に巨大化していくことである。要するに勝ち組と負け組の差が指数関数的に拡大して前者が後者を凄まじい勢いで食い殺して行ってしまうわけで、それこそが格差問題の本質であったわけということである。
この場合にしても、もし社会が太陽系型なら小さな惑星が一個や二個消滅してもそれは必ずしも天体系の質的な劣化を意味しないが、現実の社会ではそれら弱小勢力の間の相互依存関係は一種の毛細血管を作っていて、そこを資金がくまなく流れることで健全な社会が維持されている。
ところが縮退が進むと、社会の中の資金の流れが次第に巨大企業と巨大機関投資家の間だけで短絡した経路を作って、その狭い世界の中だけを高速で回転するようになり、血液が回らなくなったその外側の世界はだんだん壊死していくのである。
そしてこの問題に関しては10月号で述べたことが重大な意味をもっている。それは、作用マトリックスの固有値が実数か虚数かで、系全体の振る舞いのベース・パターンが「指数関数的(爆発的に拡大)」になるか「三角関数的(周期的に復元)」になるかが分かれるということであり、そして社会が振り子のような復元力をもって「神の手」のように長期的に安定するためには、基本的に系が後者だけで構成されていることが必要なのだということである。
実は過去の思想家たちが太陽系を眺めて「神の手」の調和を確信したとき、彼らは太陽系に残って周期的な楕円軌道を描いている惑星(これは三角関数で表現される)の存在だけを見て、残りの潜在的な半分、つまり双曲線軌道(これは指数関数をベースに表現される)を描いて宇宙の彼方に飛び去ってしまったもののことを忘れていたようである。
つまり二体問題の場合でさえ、距離が指数関数ベースで一方通行的に拡大してしまう隠れた部分の存在を考えねばならなかったのだが、三体問題以上の複雑な系ではそういう指数関数的に爆発する不安定な部分がさらに頻繁に侵入してきてしまう。
要するにこれが、経済の世界で勝ち組巨大企業と地方の弱小企業の格差を指数関数的に拡大させていったことの数学的本質だったわけだが、話はそれで終わりではなかった。それは、そのようにして勝ち組の中だけを回り始めた巨大マネーの流域はさらに狭く縮退していき、もはやモノを作ったり買ったりする世界自体を外側に取り残してさらに内側のコア、つまりコンピューターの中の瞬間的な売買で自己増殖を行なえる投機市場の世界の中だけを回り始めてしまったのである。
いわば縮退の重力場が世界中の富をブラックホールのように狭い領域に吸い込んで超高密度に凝縮させていたわけで、最後の段階ではその無意味に自己増殖したマネーの総額は、世界経済の本来のサイズの実に3倍以上にも膨れ上がっていた。しかしその内部は基本的に「神の手」の自動安定機構とは正反対の指数関数的世界で、そこに吸い込まれた世界の富は皆その性質に染まり、そしてそれまでの全ての錯覚の終曲のように、それは最後に自身を超新星のように大爆発させ、すでに半ば壊死していたその外側の世界をも爆風で襲って世界の全ての人々を巻き込んでしまったわけである。
要するにそれら全ての根に天体力学から発する錯覚が横たわっていたというわけなのだが、考えてみると米国の複雑系やサンタフェ研究所こそ、そのことを研究の最優先課題に置いて世の中に主張・警告すべきではなかったのか。しかし当時の彼らはそれを行なうどころか「複雑系で株価を予想して金融工学に役立てる」などということを言っていたのだから、それだけでも複雑系という学問は失敗の烙印を押されても仕方があるまい。
そもそも複雑系というものは何か全く新しい学問であるかのように喧伝されていたが、要するに三体問題のパッケージだけを新しくしてそう見せかけたものに過ぎず、その本質がぼやかされたことがむしろこれらの錯覚を助長させることに一役買っていた可能性が高い。そう考えるとこの際それを断ち切る意味でも、もはや「複雑系」という名称自体を廃止してあくまでも「三体問題」を表看板とし、その中に編入する形でこれらの学問全体を再編成していくのが正しい道ではないかと思えるのである。
いずれにせよもう一度、直観的に理解できる形で三体問題について考えてみるということは、前にも増して重要なことになりつつあるのは確かであり、それがタイトルをこのようなものとした所以である。では次号以降、あらためてそれについて論じていくことにしよう。




