ヒトゲノム計画で、人間のゲノムがいくつあるかということが調べられた際に、その個数が意外なほど少なく、ハエとさほど大差がないものだということが判明し、それは世の中に大きな衝撃を与えた。
　しかしそれは確かに衝撃であるには違いなかったが、実はそこに隠されていた真の意味は、むしろ世の中が驚いていたこととは正反対のことだったのである。
　もっともそれは世間の側が錯覚したというよりは、そもそも当時どうやらその重大な数学的意味を、サンタフェ研をはじめとするほとんどの複雑系の研究者自身が気づいていなかったらしく、そのためとにかくそれについて数学者サイドから何のコメントも出されなかった。
　それゆえいまだに世の中はその真の意味を知らないのであり、そのためここでそれをあらためて指摘していくことにしよう。
　ではその重要なこととは何かと言えば、それは次の意外な事実である。すなわちそれは

・一般に複雑多様な振る舞いをする系の構造を解析する場合、意外にも構成要素の個数が少ない系の方が、要素個数の多い系よりも解析が難しい。

という大きなパラドックスである。（無論遺伝子などの場合、ゲノムの個数が「構成要素の個数」である。）
　ではなぜそんなことが生じるのだろうか。その理由は作用マトリックスを用いれば一目瞭然で判明する。
　すなわち全般的な傾向として、もしある系が、確かにその振る舞いは複雑多様なのだが、同時にその構成要素の個数もまたそれに比例して非常に多いという場合、その作用マトリックスのパターンは、実は上三角型のものである可能性が十分にありうる。
　本来ならば、上半分にしか相互作用成分が存在しない上三角型の系の場合、おのおのの相互作用の糸がすぐに単純に行止りになってしまう関係上、あまり複雑な振る舞いのパターンを生成することはできない。しかしもし系の構成要素の個数が多いならば、その個数自体に物を言わせて、振る舞いの多様性を作り出すことが一応は不可能ではないからである。

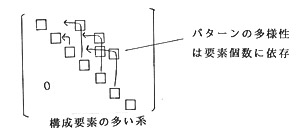
　△図１

　一方それに対して、もしある系の構成要素の個数を調べたところ、それが非常に少なかったにもかかわらず、最終的な振る舞い自体には非常に複雑な多様性が生じている場合、作用マトリックスが上三角型であっては、それだけの多様なパターンを生成することは到底できない。
　つまりこの場合、その系の振る舞いの多様性は、原理的に作用マトリックスの下半分にある相互作用成分それ自体の力に依存する以外にないはずである。（しかもそれは線形であったのでは、必ずしも十分な複雑多様性を作り出すことができないので、それらの演算子はスイッチ演算子がついている可能性が高い。）

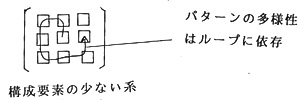
△図２

　要するにそれは、系全体がどうしても三体問題型でなければならないということを示しているのであり、そしてひとたび系が三体問題型だということになれば、その振る舞いのパターンの個数は一挙に指数関数レベルに増大して、系の解析はちょっとやそっとのことでは不可能になってしまうというわけである。

　つまりこうしてみると、系の構成要素が少ないから解析が楽だと思うのは完全な錯覚だったのであり、むしろ構成要素の個数が少ないことは、系が上三角型の系である可能性を否定してしまうために、逆に解析が難しいことを証明する結果になるという、実に大きなパラドックスが存在していたわけである。
　例のヒトゲノムの話では（筆者の知る限り）、このパラドックスは全く数学者によって指摘されず、それゆえヒトのゲノムの個数が意外に少ないことが、話を楽にするどころか全く逆に、遺伝子解析の困難さを証明するものであったことに気付いていた人は、ほとんどいなかったようである。

単純なゲームはなぜ面白い
　そしてわれわれは実はこのパラドックスを、別のかなり身近なところでも見ることができる。それというのもこのことは、一般にいろいろなゲームというものをやってきた人にとっては、無意識のうちに理解されていることなのである。
　チェスや囲碁などを含めて、広くゲームというものについて知っている人は、次のことを知っている。すなわちそれは、

・一般にゲームの世界においてはルールが単純なものほど奥が深くて面白い

ということである。
　そしてこのこともまた、先ほどと同じ論理に基づいている。すなわちやたらに複雑にルールを作り込んでいるゲームというものは、結果的に見ると系全体が上三角型の構図になってしまっていることが多いのに対し、ルールの単純なゲームは、そのパターンの多様性を相互作用成分の力の側に依存する三体問題型になっていることが多いからである。

　大体においてゲームというものは、そもそもプレーヤーたる人間がルールを理解しなければ成立しないものなのだが、一般に人間が記憶できるルールの個数というものには上限があり、そしてルールの個数とは作用マトリックスで言えば、要するに相互作用成分の個数のことである。
　つまりおよそゲーム全般を作用マトリックスで表現していった場合、その相互作用成分の個数には共通した一定の上限があるわけである。
　ということは、ルールすなわち構成要素の個数を多くしてしまうと、上半分にたくさん相互作用が生じてしまう関係上、それだけ下半分の成分をゼロにして減らさなければ人間の認識能力を超えてしまう理屈になる。
　つまりこの場合、ルールの個数を無闇に増やしても、その増やしたルール１個あたりが新たに作り出す相互作用の糸が、閉じたループを作れず上半分だけで行止りになってしまいがちなのである。
　一方逆にルールすなわち構成要素の数が少なければ、作用マトリックスの下半分にある相互作用成分が全部生きていても、人間はルール自体の認識は一応できるので、ゲームとして十分成り立つことになる。
　実際、特に囲碁などの古典的なゲームをみると、その多様性のパターンは、下半分を含めた相互作用成分全体が作るループによって、発生していることがわかる。

　そしてまさにここで作用マトリックスは、重大なことをわれわれに伝えることになる。つまりこの結果どうなるかといえば、前者の場合にはそのゲームがつくる宇宙はたかだか可算無限個のパターンの多様性しかもたないが、後者の場合にはそのゲームがつくる宇宙は、非可算無限個のパターンの多様性を持ち得ることになるということである。
　それゆえ読者がもし、単純なゲームの方が奥が深くて面白く、そこに宇宙さえ感じることがあると感じたことがあったとすれば、その背後には実はこのような数学的メカニズムが隠されていたわけである。

　そのことを含めて、このパラドックスは極めて基本的かつ重要なことであるにもかかわらず、世の中に十分理解されていないという点で、ちょっと珍しいものであると言えるだろう。