ラグランジュ点問題の直観的方法
「物理数学の直観的方法」第2版では、加筆した11章で三体問題について論じたが、ラグランジュ点の問題に関しては面白くはあるものの、それがもともと三体問題の中の特殊例に過ぎないこともあり、枚数の関係からひどく簡単にしか述べることができなかった。
そこで、本には書けなかったその「ラグランジュ点問題の直観的方法」について、ここで述べてみようというわけである。(なおこの部分は、本の内容とはほぼ完全に独立して読める。)
以下の内容は大きく
1・ラグランジュ点の簡単な概要
2・ラグランジュ点はどのように釣り合っているか
3・なぜそこには復元力が生じるのか
に分かれている。
なおこの稿の前半部分(1と2の前半ぐらい)の内容は単なる簡単な概説なので、他にも書いてある本は多いと思われるが、後半以降(主として3)の部分は、かなり思い切った方法でラグランジュ点の不思議なメカニズムを直観的に把握することを試みたものであるため、それは恐らくこれまで(筆者の知る限り)他の本−−英文の本を含む−−では読むことのできなかったものであり、その意味で貴重なものであるはずである。
それゆえ関心のある方は、2と3についてはプリントアウトしてじっくり読むことをお勧めする。
(20010120 長沼伸一郎)
・ラグランジュ点の基本的な構図
・木星とトロヤ群
・コロニー計画への利用価値
さてラグランジュ点の基本的な構図については、読者の多くはご存じと思うが、一応述べておこう。
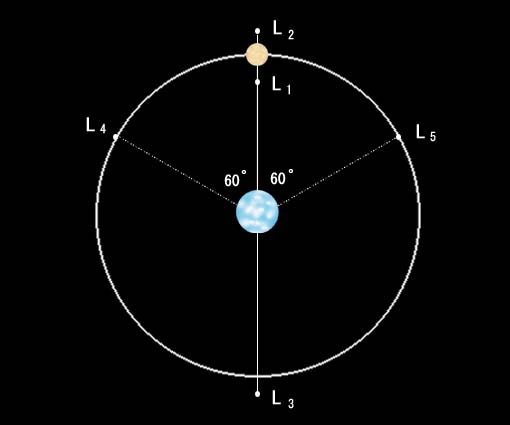
一般にラグランジュ点は5個所に生じ、それは図のL1からL5の5個の位置である。

このうち直線上に並んでいるL1、L2、L3の三つは不安定であり、この位置にある小天体はちょっと位置に誤差が出るだけで、すぐにそのずれがどんどん大きくなってしまって、やがてこの位置から外へ出てしまう。
一方正三角形の頂点の位置にあるL4とL5は安定で、ごく僅かに位置がずれても元に戻すよう復元力が働いている。
ただしこれが安定であるためには、正三角形の共通底辺をなす二つの天体(例えば地球と月)の質量比に制限があり、小さい方の質量が大きい方の1/25.8以下でなければならないとされる。(なお月の場合、その質量は地球の1/81.3である。)
ラグランジュ1772年にこのことを計算して発見したときには、単に数学上の面白い解に過ぎないと思われていたが、その後20世紀に入って天体観測が進むにつれて、現実にその例が見つかっていった。
それは木星の軌道上においてのことであり、太陽系の惑星の中でも木星の質量は飛び抜けて大きいため、こういう影響が生じる可能性が現実に存在していたのである。
そして木星と太陽を底辺とする正三角形のL4とL5の位置に複数の小惑星が発見され、ここにそれらが存在するのはラグランジュ点の力学ゆえに相違ないと確信された。
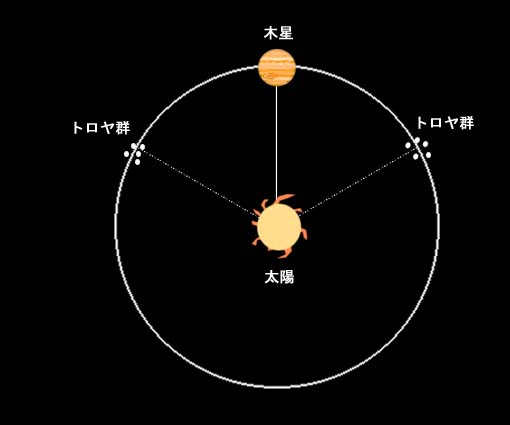
なお木星の場合、それらの小惑星群は「トロヤ群」と命名されているが、そのネーミングの由来は、それらの各小惑星にそれぞれアキレスやパトロクロスなどといった、叙事詩「イリアス」に登場するトロヤ戦争の英雄たちの名前がつけられていたからである。
さて現実の天体の例としては木星の場合しか発見されていないが、しかし理論的には地球と月も十分にその条件を満たしており、ここでもそういうことを考えることは十分可能である。そこで、スペース・コロニー計画でそれが脚光を浴びるようになったというのは、よく知られたことである。
もっとも、現実にコロニー用に使えるのは正三角形の頂点のL4とL5だけであり、残りの三つは常に人為的に修正を続けていかねばその位置を保てない。そのため後者の場合は、ごく小さな人工衛星をそこに置いて短期間だけ月にとっての「静止衛星」として使うならともかく、巨大なコロニーや小天体だと修正用の燃料代も馬鹿にならないだろう。
一方安定な正三角形のラグランジュ点(L4、L5)の場合、それは単に釣り合うというだけでなく、そこには復元力が働くという非常に興味深い特性があって、それがこの場所を利用する上での大きな魅力となっている。それはちょうど、海の上にサルガッソー海のように海流が集まって停溜する特殊な海域があって、そこに海藻や浮遊物を集めてしまうのに似ている。
この特性ゆえここは、複数のコロニーを密集状態で集めて外に漂い出さないようにしておくには絶好のポイントとなるわけである。ただしこの場合のイメージに誤解のないよう言っておくと、「海流が停溜する」といっても、それは水域内部に完全な静止状態を作るということではなく、この中にある各コロニー同士の距離にしても、常に一定不変で相対的に静止しているわけではない。
むしろここにはたらく「復元力」は、小天体などをこの中で非常に長い周期でゆっくり振動運動させることで外へ出て行かないようつかまえておくという性格のものだから、実はコロニー相互の位置も(ちょうど停泊中の船同士の距離が、うねりや潮位に動かされて僅かに変動するように)非常にゆっくりと周期的な変動を繰り返していることになる。
ところがこの復元力がどうして作用するのかを直観的に理解したいと思っても、従来それは難しすぎてほとんど不可能だったように思う。そこで、この稿の後半部分ではそれを解き明かしてみようというわけである。
・ラグランジュ点の釣り合い
・L4とL5の基本的な構図
・三角形の軌道が釣り合う条件1
・三角形の軌道が釣り合う条件2
さて「物理数学・・・」の11章「三体問題と複雑系の直観的方法」で述べたように、作用マトリックスN乗理論は、スイッチ演算子の考えと組み合わせると、(三体問題も含めた)非線形方程式に対して時にほとんど最終兵器に近いほどの威力を発揮する。
実際三体問題の場合、例えば「制限三体問題」として例外的に解けるケースは全体の中ではどのぐらいあるのかなどという問題に関しては、これを用いれば原理的にすべてを洗い出して決着をつけてしまうことが可能である。
しかしその一方、しばしばその結論は大づかみでありすぎて細部がわからず、ラグランジュ点の場合も、具体的に天体力学の観点からどのように安定状態を作るのかと問われても、この理論ではあまりよくわからない。
そこで以下に古典的なやり方で、ラグランジュ点がどうして生じるのかについて見てみることにしよう。
まず5つのラグランジュ点がどうして生じるのかであるが、このうち直線上に並んでいるL1、L2、L3の3つに関しては、大体このあたりに釣合い点(安定か不安定かは一応別にして)が生じるであろうということは、直観的にも十分理解できる。
この場合要は、その位置にある小天体がこの角速度で地球の回りを回っていていても遠心力と引力が釣り合えば良いのである。例えばL2の場合、普通なら地球からこの距離にある小天体がこの角速度で円軌道を周回することはない。
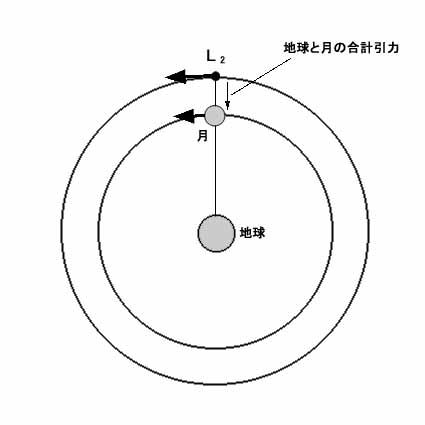
実際この角速度では、本来なら遠心力が強くなりすぎて地球の引力を上回り、小天体はもう少しゆっくり周回するのでなければこの軌道を保つことができない。
しかし間に月があることによって、この位置には地球と月の引力の合計で通常より強い引力が働いており、その遠心力と釣り合いをとることが可能となるのである。
そして一直線上に並んだあと二つのL1とL3についても、基本的に同じメカニズムでそのあたりに釣合い点が発生するわけである。
さてそれでは正三角形の頂点の位置にあるL4とL5に関してはどうだろうか。こちらは多少複雑であるが、それでも釣合いの基本的な構図を見ることそれ自体は、そんなに難しいことではない。
これを見る場合、まず基本的に次の点に注目しておくとわかりやすい。それは一般に複数個の天体を考える場合、その運動は基本的に天体系の重心位置を基準点に展開されているということである。
そして小天体の質量を非常に小さいと仮定した場合(ラグランジュ点の問題は普通そういう仮定を置いている)、天体系全体の運動の基準点となる重心点は、地球と月を結んだ線上、その長さを地球と月の質量比で区切った位置に生まれていることになる。
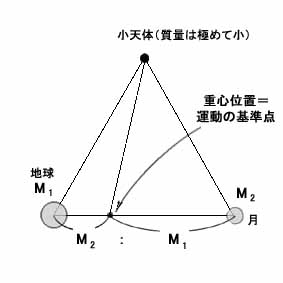
そして小天体の軌道に関しては、次の二点がクリアされているかどうかを確かめれば、一応は釣り合うかどうかがわかることになる。すなわち
条件1・小天体にはたらく地球と月の引力の合力ベクトルが、正確にその重心点の方向を向いているか。
条件2・小天体が発生する遠心力(ただし重心点から小天体までの距離をその円運動の半径とみた場合)が、地球と月の引力の合力ベクトルの大きさと正確に釣り合うか。
の二点について見てみればよい。以下、それを見ていこう。
まず条件1については、小天体の位置が正三角形の頂点、あるいは少なくとも二等辺三角形の頂点にあれば、これはクリアされる。
つまりこの場合、まず三角形の等しい二辺はここでは小天体から地球および月までの距離に相当しており、それが等しいというのだから話は簡単になる。
要するにどうせ距離が等しいというなら、地球と月の引力の比較の際にrの2乗の計算の必要がなくなり、それぞれが小天体に及ぼす引力の大きさの比は単に両者の質量の比だけで決まってしまう。つまりそれを表わす2本のベクトルの長さの比は、地球と月の質量比に等しいわけである。
そして一方先ほどみたように、重心点の位置が地球と月を結ぶ線上のどこにあるかもやはり両者の質量比で決まっているため、作図をしてみるとベクトルは結局必ず重心点の方向を向いてしまうことがわかる。
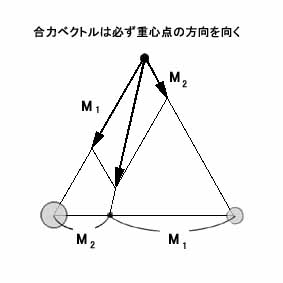
つまり天体の位置関係が正三角形か、あるいは少なくとも二等辺三角形であれば、まずこの条件1はクリアされることになるのである。
・三角形の軌道で釣り合う条件2
さて次に条件2、すなわち遠心力の大きさ自体がちゃんと釣り合うかという点であるが、ここでは問題を簡単にするために、底辺の二天体の質量を完全に等しいと仮定して考えてみよう(なお小天体の質量はやはり非常に小さいものとする)。
つまりこの場合、重心点は底辺の二つの惑星を結ぶ線上のちょうど中点に存在することになる。
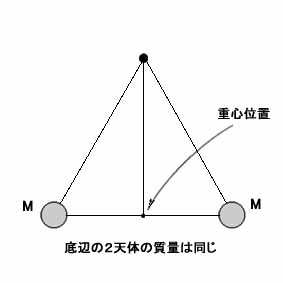
ここまで問題を単純化すれば、同じ周期の角速度で力の大きさが釣り合うかどうかは比較的簡単な計算で確認することができる。
ただしこのとき一つ錯覚しないよう注意すべきことは、底辺にある二つの惑星についてその遠心力や角運動量などを考える際には、その円運動の「半径r」は惑星間の距離そのもののことではなく、重心点からそれぞれの惑星までの距離(つまりこの場合は惑星間の距離の半分)のことであり、こちらを半径rとして遠心力などを計算すべきだということである。
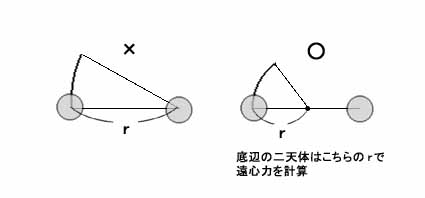
言うまでもなく小天体の場合も同様で、こちらも重心点から小天体までの距離を半径rとみて遠心力などを計算する。
そして正三角形ならば作図をしてみれば(慣れた人なら暗算でも)、小天体の周期ないし角速度が底辺の両惑星の円運動のそれと等しければ、ちょうど頂点の位置で引力の合力と遠心力が釣り合うようになることがわかる。
これは簡単なので、練習問題として各自試みられたいが、不慣れな人のために一応解答も以下に示しておく。
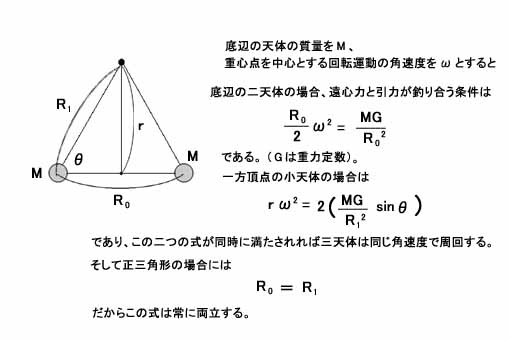
そしてもっと一般に、底辺の二天体の質量が同じでなく、重心位置が中点にない場合でも基本的に同じである。
以上よりこの場合、小天体に作用する力のベクトルは方向、大きさの両面で共に一応は釣り合うことがわかったわけである。
ただし条件2の場合、条件1の時とは違って二等辺三角形ではこの関係は成立しない(それは直観的にも明らかである)。つまり条件1だけでなく条件2も満たすことが要求された時点で、三天体の位置関係は正三角形に限られることになる。
・ラグランジュ点の最大の不思議
・編隊飛行のアナロジー
・ラグランジュ点への適用
・通常の円軌道の場合
・三種類の軌道の序列
・復元力のメカニズムの秘密
・復元力の実際
・なぜ質量比の制限が生じるか
・周囲の浮遊物を集める力
では次にこのメカニズムのもう一段深いところを見てみよう。それはある意味でこの話の最も謎な部分、すなわちラグランジュ点の復元力の不思議であり、直線上に並んだ3つのラグランジュ点(L1、L2、L3)は不安定なのに、なぜ正三角形のラグランジュ点(L4、L5)だけには復元力があって安定で、周囲に浮遊している小天体をこの点に集めてしまうのかという問題である。
実のところこれは、意外なほど多くの人が知りたいと願いつつも果たせずにいる、隠れた難問題ではあるまいかと思われる。
しかし計算の細かいところまで話をすると、やたらに込み入って複雑になるので、あくまでこのメカニズムの本質を直観的に把握することを主眼とし、あまり細かいところは省くことにする。
まあ大体において釣り合いの問題というのは、複数の要素や力が微妙に組み合わされて結果的に釣合い点が生じているという場合が多い。そのためそれをシャープに一つの視点だけに絞り込んで直観的に理解させるというのは、本来無理と言えば無理な要求なのであり、他でもないラグランジュ自身、そんなことを求められても困惑したことだろう。
だがここではそれを承知の上で、敢えて本質の直観的理解に挑むことにするので、そこらへんの事情は了解されたい。多少難しい部分はあるかもしれないが、基本的には大学一年の物理の知識だけで理解できるよう工夫されており、何よりもこれは今まで、結構な大家といえども敬遠して具体的な理解を諦めることの多かったものであるだけに、挑戦する値打ちは十分にあるはずである。
さてまず最初に言ってしまうと、そのメカニズムを作り出す根本原因は角運動量保存則にある、などといっても、多くの読者はそんなことを言われても頭が混乱するだけであろう。そこで難しいことはこのさい忘れて、次のようなイメージを基本に据えて以下の話を進めていこう。
もし読者がパソコンのフライト・シミュレーター、特に編隊飛行ができるものをいじったことがあるとすれば、以下の話は感覚的にも非常にわかりやすくなる。そのためそうでない読者も、一応それを頭に思い浮かべていただきたい。
一般に、ある飛行機が編隊を組んで飛んでいるとき、自機の高度や速度は常に一定というわけにはいかず、それは上下動を繰り返して、編隊の他機との距離も近くなったり遠くなったりを繰り返しながら飛んでいる。
そしてこのとき計器盤を眺めていると、例えば知らない間に高度計の針が上がってしまって自機の高度が編隊の定位置より上に出てしまっているときには、位置エネルギーが大きくなった代償として、速度計の針は少し下がっているのが普通である。
つまり高度と速度の間には、一方が上がればもう一方が下がるという関係があるわけだが、この特性は編隊飛行においても実際によく利用されている。
例えばもし自機の速度が何かの理由で一時的に遅くなってしまい、気づいた時には編隊より遅れてかなり後ろの位置を飛んでいた場合、編隊に追いつこうと思ったパイロットは、エンジンのスロットルを下手にいじるよりも、むしろ大抵はこれを用いて距離を詰めることを行なうものである。
つまり普通こういう時にはパイロットは操縦捍を少し前に倒して高度を下げ、編隊より少し下の高度まで降りていく。するとだんだん速度計の針は上がって行って、やがて編隊に後方斜め下から接近して追いつくことができる。そして十分近づいたところで元の高度に上っていけば、ちゃんと編隊の中に戻ることができるわけである。
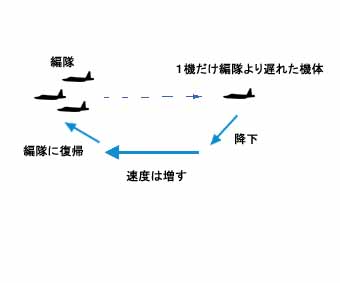
これとは逆に、自機が速度をうっかり出しすぎて編隊より前の位置に出過ぎてしまっている時には、パイロットは操縦捍を心もち引いて高度を上げ、編隊の定位置よりやや上に出れば、速度が落ちてやがて元へ戻れる。
航空機の場合はこうしたことは実に日常的なことだが、ところで天体力学の場合にも実はこれと似たようなことが起こっているのである。
そして天体力学の場合、それはケプラーの「面積速度一定の法則」という形で現われている。つまり一般に楕円軌道の上の天体は、低い位置に落ちていくにつれてその角速度が大きくなり、結局単位時間に天体がスイープする扇形部分の面積は、常に一定になるという法則である。
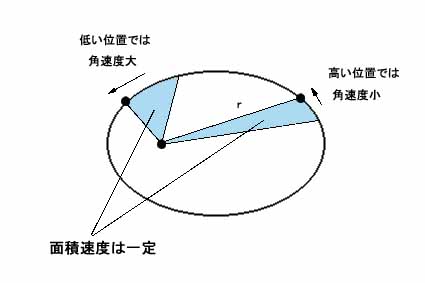
この場合、軌道半径を「高度」と解釈すれば、先ほどの飛行機の話と良く似ていることがわかるだろう。もっとも厳密には少しメカニズムは違うのだが、それでも「高度が下がると速度が上がる」という現象自体は、位置エネルギーと運動エネルギーの関係で起こっているため、少なくともその点では基本的に同じことである。
では以上を頭に入れた上で、ラグランジュ点の安定性の話に移ろう。それは基本的には次のような話を考えればよい。
つまりこの場合、ラグランジュ点にある小天体群やコロニー群が、ちょうど編隊のようにして同じ角速度で軌道上を「飛んで」いるとイメージし、ある1個の小天体がその編隊から遅れてしまったとき、その小天体は自動的に編隊に追いつけるか否かという問題を考えればよいわけである。
そしてこの場合、小天体が編隊から遅れて距離が開きつつある時には、言うまでもなくその小天体の角速度は少し小さい値になっている。そして小天体は軌道上で角速度が遅くなると、当然ながら少し落下して高度が落ちるが、そうやって高度すなわち位置エネルギーを失っていくにつれてやがて速度は回復し、再び上昇に転じていく。
つまり問題の要点は次の点にあることがわかる。すなわちこの小天体の高度が落ちていく場合に、もしその過程で小天体がもらう運動エネルギーや角速度の最終的な合計が、非常に都合の良い絶妙の大きさになってくれていれば、やがて編隊に追いついてそこに戻ることができるし、逆にそれが適正値から大きく外れた値になっていれば、小天体は編隊には戻れずどんどん離れていってしまうということである。
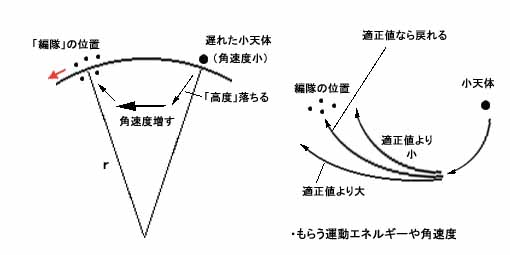
つまり安定なラグランジュ点の付近では恐らく前者のようなことが起こっており、一方不安定なラグランジュ点の付近では、後者のようなことが起こっているのではないかと想像できるというわけである。
・通常の円軌道の場合
なおラグランジュ点について調べる場合、まずそれに先立って、普通の天体系の場合にはこのあたりのことがどうなっているかをきちんと頭に入れておく必要があるため、ここでそれを述べておくことにする。
要するに一番単純な円軌道の場合には、今の話はどうなるかということであるが、ここでは話をさらに簡単にするため、とりあえず月の存在を除外して、地球と人工衛星だけの単純な問題でこれを考えてみよう。
そして例えば2個の人工衛星が、ランデブーして隣合った状態で円軌道上を一緒に回っていたとき、その片方が何かで角速度を少し失ってしまったら、両者の位置関係がどうなっていくかということについて考えればよい。
こういう場合、角速度が小さくなった衛星は当然ながら楕円軌道に入って落下していくが、1周すればやがて元の位置に戻ってくる。
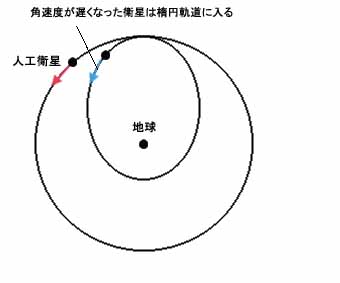
しかしそれならこの衛星が元の位置(遠地点)に戻ってきたとき、ちゃんと元通りにもう一方の衛星とランデブーできるかといえば、そうではない。なぜならこの場合、楕円軌道に移行した側の周期が変わってしまって同期がとれなくなるからである。
具体的に言えば、その状況は天体の周期に関するケプラーの法則、つまり「周期の2乗は楕円の長径の3乗に比例する」を使えば容易にわかる。
つまりこの場合、楕円軌道に入った衛星の方は(軌道の長径が少し短くなるので)多少周期が短くなり、その衛星が再び遠地点に戻ってきた時には、円軌道の側の衛星はまだその位置に来ていない。つまりこれを編隊飛行の話に置き換えて言うと、編隊から遅れた機体は一旦高度を下げてから再び戻ってきた時に、逆に編隊より少し前に出てしまっていることになるのである。
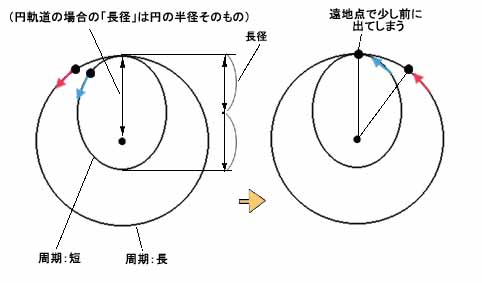
そして両者の位置関係は1回ごとにそれだけずれていくから、角度のずれはどんどん大きくなっていく。
このように、一般に円軌道の場合を復元力という観点からみると、それはr方向(編隊飛行なら上下方向)に関しては、振動するような形で復元力が働いて安定だと言えるが、角度方向(編隊飛行なら前後方向)に関しては、不安定とまでは言えないにせよ、とにかく復元力は働いていないことになるわけである。
まあそれでも現実問題としてみると、円軌道の場合は角度方向に少しぐらい位置がずれても(その天体を暦に利用しているなどの場合を除けば)それはほとんど問題にはならないし、多くの場合は気づかれもしない。
しかし正三角形ラグランジュ点の場合はそれでは困るのであり、角度がだんだん狂っていくようでは到底正三角形の頂点の位置を維持できず、軌道そのものの崩壊につながってしまう。
それはともかく、こうしてみると三種類の軌道、すなわちA:安定な正三角形ラグランジュ点、B:通常の円軌道、C:不安定な直線上ラグランジュ点の三者は、復元力という点で恐らく次のような序列にあると推測できる。つまり
A・安定なラグランジュ点(正三角形) :r方向、角度方向とも復元力あり
B・通常の円軌道 :r方向には復元力あり、角度方向には復元力なし
C・不安定なラグランジュ点(直線上) :r方向、角度方向とも復元力なし
という具合に、CからAに行くにしたがって次第に復元力が増していくという序列である。
さてそうだとするとこれら3つのケースにおいては、天体間に働く力の何が違っているためにそういう序列が作り出されのだろうか。
それを見るためにここでは問題を単純化し、小天体が重心点方向に距離hだけ落下した時に、おのおのの位置での引力の強さ(地球と月の合計分)の大きさがどうなっているかをA、B、Cのそれぞれについて簡単なグラフにしてみよう。
そしてここで結論を先に言ってしまうと、その際にグラフのカーブが急であるか緩やかであるかという割合に単純なことが、この序列を作る原因になっていると考えられるのである。では具体的に、各位置での地球と月の合計引力値が三者でどうなっているかをグラフで比較してみよう。
まず最初に一番不安定なC、すなわち直線型のラグランジュ点の場合から見ていくと、例えば一番遠くにあるL2の場合、ここでは高度による引力の変化率が通常よりも大きくなっていることがわかる。
すなわちこの位置にはたらく引力の値は地球と月のそれの和であるが、高度がhだけ落ちた時には、地球からの分はR−hの2乗に反比例して増えるのに対し、月からの分はr−hの2乗に反比例して急激に増えている。
つまり合計引力のうちの一部が急なピッチで増えるため、この位置では通常の場合に比べて重力変化のカーブはきつくなっているわけである。(なおうるさいことを言えば、このときの「通常の場合」というのは、要するに月を考えないかわりに少し地球の質量を大きくして、この位置の重力の強さをちょうど同じ値にしてやった場合のことである。)
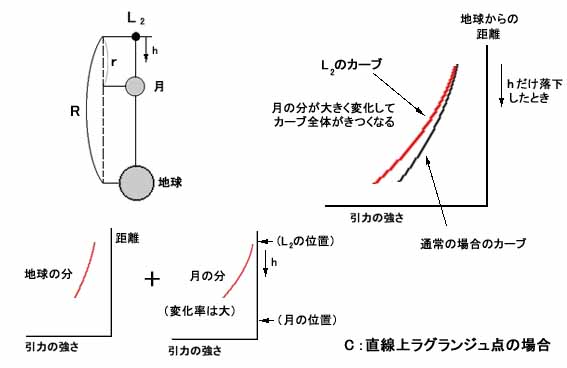
では今度は一番安定と考えられるAの場合はどうだろうか。実はこの場合には話はちょうど逆であることがわかる。
つまりこの場合、月の分の引力はいわば側面から作用しているため、小天体の高度が重心点方向にhだけ下がった場合でも、小天体から月までの距離そのものは相対的に少なくしか変化しない。
そのため月の分の重力変化(距離の2乗による)は、先ほどとはちょうど逆に小さくしか効いてこず、そのため合力のベクトルの大きさは(たとえ月への角度が僅かに変化することの影響を加味しても)、通常に比べて変化が小さい。つまり重力変化のカーブは通常よりも緩やかになっている。
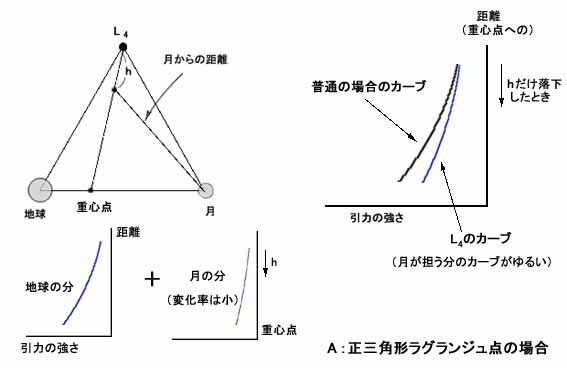
このように重力変化のグラフを並べてカーブを比較すると、Cが一番変化がきつく、Aに向かうほどカーブが緩やかになっていることがわかる。つまりはそれが復元力の強さに関して先ほどのような序列ができる原因だと推察できるわけである。
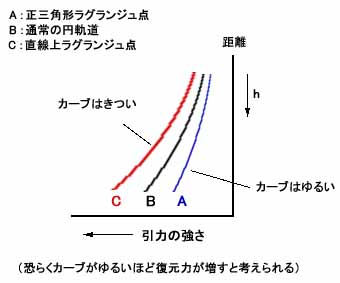
では本当に重力変化のカーブが緩くなることが、復元力を増すことにつながっているのだろうか。しかしこの復元力の具体的な過程はやや複雑で混乱しやすいので、その直観的な把握の助けとするために、ここで次のイメージを頭に入れておくとよい。
先ほどは編隊飛行というイメージで、小天体群が円軌道上をシンクロして動いている状況を捉えたが、ここではそれを、数人のハンマー投げの選手たちが完全にシンクロした状態でハンマーを回しているというイメージで捉えてみることにしよう。
そしてここで一人の選手だけがどこかでちょっと遅れてしまい、ハンマーの位置が皆より10度ぐらい後ろにずれた状態のままで回転運動を続けていたとする。さてこのときこの選手がそれを修正して皆と同じ位置にハンマーを戻したいと思ったら、どうすれば良いだろうか。
こういう場合にはこの選手は、一旦ワイヤーを力一杯ぐいと引いてハンマーを手元に引き寄せ、その後再び力を抜いて遠心力のままに元に戻せば良い。そうすれば、ハンマーが引き寄せられて回転半径が短くなっている間は角速度が少し早くなり、戻すタイミングや引く力の大きさをうまく加減すれば、うまく皆に追いつくことができるというわけである。
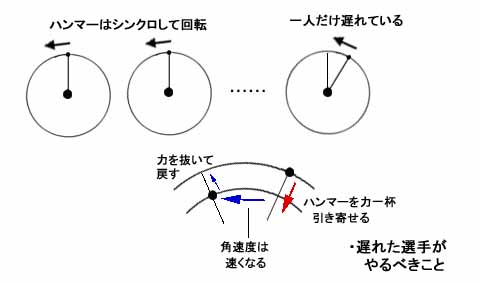
そしてこのイメージを普通の天体の円軌道の場合(先ほどのB)に適用してみると、実はこのとき、その力の加減は必ずしもうまくいっているとは言えないことになる。
つまり先ほどの二つの人工衛星の話では、二つの衛星はランデブーに失敗してしまっていたが、それをこのイメージを使って言うと、どうやらこのときの「ワイヤーを引く力」は適正値をオーバーしてしまっているらしく、力を抜いて元へ戻した時にはハンマーの位置は逆に少し前へ出過ぎているのである。
そのためちょうどぴったりした位置に戻したい場合、ワイヤーを引き寄せる力を少し弱めに加減する必要があり、つまり腕の筋肉の仕事量が少し小さくなるようにすれば、少し引き寄せただけですぐに遠心力に引き戻され、結果的にうまい位置で元に戻るということになる。
そして天体の場合、「筋肉の仕事量」に相当するものは重力の行なう仕事量のことであり、それは先ほどのグラフの場合、グラフが囲む面積という形で表現されている。(「力=引力」を落下距離で積分したものが、この場合の仕事量である。念のため。)
そして正三角形ラグランジュ点(A)と通常の円軌道(B)のグラフを並べてみると、高度が下がっていくときに重力が行なう仕事は、次の図に示した部分の面積として示されており、左側すなわちラグランジュ点周辺の方が、カーブが緩くなっている分だけ面積が小さい、つまり仕事量は少なくなっていることがわかる。
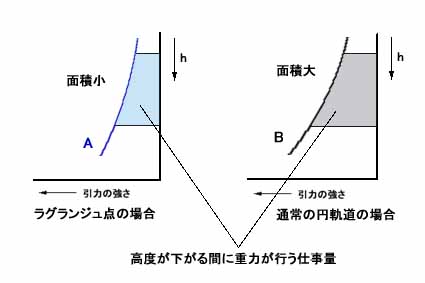
それゆえ通常の円軌道の場合に比べると、ワイヤーを引き寄せるときの筋肉の仕事量がやや小さめに加減されていることになり、ちょうどよい位置に戻るような形で復元力が働くというわけである。
要するにこれが、なぜ正三角形のラグランジュ点では復元力が働いて、そこに小惑星などをつかまえておけるのかという謎への答えだったわけである。
ただしこれも過ぎたるは及ばざるが如しで、重力のカーブがあまり緩くなりすぎると、今度は角度の戻り方が不足して編隊の少し後ろの位置に戻ってしまい、せっかく一旦高度を下げてから戻ってきてもまだ編隊に追いつけないということになりかねない。
そして特にラグランジュ点の場合、編隊から離れた位置にあまり長いこと留まっていると、知らず知らずに月の引力で流されてしまうので注意が必要である。
実際そのように、追いつくための回復動作を何度も失敗し、そのやり直しを月に寄り過ぎた位置で呑気に繰り返していた場合、その位置では本来よりも月の重力が強くなっているので、長時間留まっていると、気がついた時には月方向にかなり引き寄せられていて、ついにはラグランジュ点の微弱な復元力では引き戻せないところまで流されてしまう。
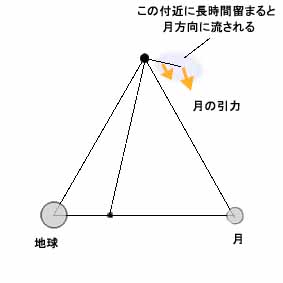
それゆえ本来なら復元力の議論にしてもこの力の影響を無視するわけにはいかず、少なくとも第二要因としての地位を与えて、先ほどの要因と組み合わせて全体を見ていくべきではあったのだが、ただそれをやると話がややこしくなりすぎるうえ、位置のずれが十分に小さい間は脇役として無視することが一応可能と思われたため、ここではとりあえずそれは議論からは除外してある。
まあそれはともかく、要するに編隊への復帰運動もあまり離れた位置で呑気に何度もやり直しを続けてはいけないということであり、そのため重力変化のカーブにしても、あまり緩くなりすぎるのは問題だということである。
ところで正三角形のラグランジュ点の場合、冒頭でも述べたように底辺の2天体の質量比に制限があって、小さい方が大きい方の1/25.8以下でないと復元力がうまく働かないということになっていたが、その理由の一旦も実はこれを見ると直観的に少しは理解できることになる。
つまりこの場合、月(の位置にある天体)の質量が大きくなっていって地球の質量とあまり差がなくなっていくと、天体系の重心点はだんだん中央位置に寄ってきてしまう。そして重心点が中央位置に近づくとどうなるかというと、実はそれにしたがってグラフの重力変化のカーブも次第に緩くなってくるのである。
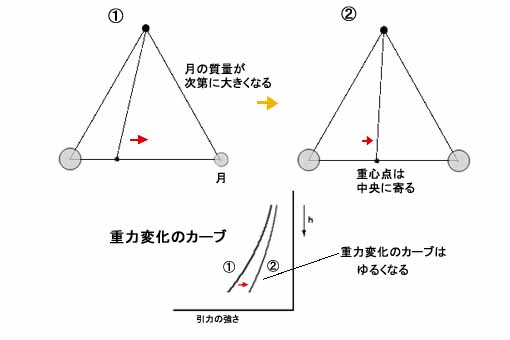
なぜカーブが緩くなるかはちょっとわかりにくいかもしれないが、一応もう少し具体的に述べておこう。
実は先ほどの3つのグラフのカーブの話などでは、もっぱら月の重力のみに関心を払っていた。そして正三角形ラグランジュ点の場合、図では重心点方向への落下の際に、落下方向と月の方向の間に角度(大体50度ぐらい)があるから、カーブが普通より緩やかになるというストーリーだった。
しかしその時の議論では、単純に言って要するに角度さえあればその天体の引力カーブは緩やかになるということだったのであり、そしてここであらためて図を見ると、地球の方向との間にも、一応10度ぐらいではあるがちゃんと角度がついている。
つまり本来なら地球と月を平等に扱って、両方で全体のカーブを緩やかにしていると考えるべきだったのである。しかし10度ぐらいではその効果は大したものではなく、話をややこしくするだけなので、いささか不平等だが地球のことについてはあえて無視していたのである。
しかし角度がもっと大きくなってくると、地球の分の貢献度も月の分に比べて甲乙つけ難いものとなり、そしてもともと地球の方が質量や重力が大きい以上、角度のハンディが緩和されていけば、ある時点でむしろこっちが主役となって、逆に月の方が単なるつけ足しの立場に落ちることになるのは明らかである。
そしてここでわれわれが問題にしている状態とは、まさにそのように地球が完全に主役になって、月がどうでも良くなっている状態なのである。(もっとも白状すると、本当は角度10度ぐらいですでにそういう状態になっているのだが。)
ともあれそれならそれで話は簡単となり、この局面に関する限りは地球だけを視野に入れて物事を考え直せばよい。そして少なくとも当面は、重心点が中央に寄って地球との角度が大きくなるほどグラフ全体のカーブは緩やかになっていく理屈であり、両天体の質量が等しくなった時点でそれは極小化するはずである。
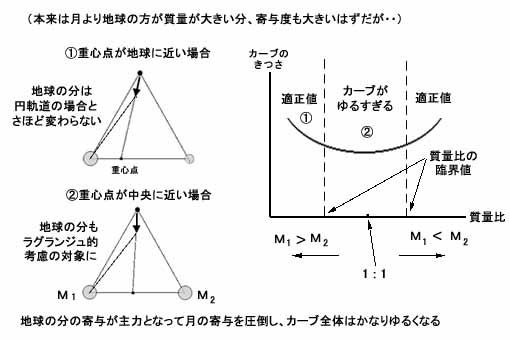
つまりそのどこかで実はカーブが緩くなりすぎていて、小天体がうまく編隊に戻れる適正値を超えてしまい、それが先ほどの質量比の臨界値として現われているのではないかという想像が成り立つことになるのである。
一般に紙の上で行なう天体力学(つまり天体の実際のデータが数値として与えられていない)において、何か特定の数値が出てくることは非常に珍しいのだが、こうしてみるとこの場合に限っては、それは十分あり得る話だということがわかる。
まあその臨界値を実際に求めるのは直観的な方法ではちょっと無理だが、ともあれそれは、正三角形の複雑な幾何学の中の釣合いに関連した量として出てきているのだということが推測できるだろう。
では話の仕上げとして、次のような問いについて考えてみることにしよう。先ほどは最初に編隊飛行というアナロジーでこの問題を捉えたが、そこでは例えば自機の位置が編隊から遅れてしまっている時には、それに先立ってまず速度の方が落ちており、その結果として位置がどんどん後ろになっているのだという仮定がなされていた。
つまり位置の遅れには必ず速度の低下が伴っていることが仮定され、それゆえにこそ天体の場合にはそれに続いて高度が下がって、一連の過程が始めるという話になっていたのである。
しかしここで次のような疑問を持たれた読者はないだろうか。それは、何かの理由で位置だけがずれてしまったらどうなるかということである。
つまりこれは、自機が乱気流などで一時的に編隊より後ろの位置に運ばれてしまったが、スロットル自体はいじっていないので、乱気流がおさまった後は、その位置で元通り編隊と完全に同じ速度で飛び続けているという状態に相当する。
そしてこれは天体の場合だと、普通この状態を続けていても(角速度が同じなのだから)高度が落ちるということはなく、これでは一連の過程はスタートせずに、位置のずれの復元も行なわれないままその状態をずっと続けることになる。
そうなると当然ラグランジュ点の場合も、位置だけのずれでは復元力が働かないのではないかという話になってくるわけだが、実はそうではなく、位置だけが角度方向にずれた場合でもちゃんと復元力は働くのである。
そしてここで、先ほどまで無視していた第二要因が作用してくることになる。要するにラグランジュ点から離れた位置に長く留まっていると月の引力で流されてしまうという、例の話である。
つまりこの場合、小天体の位置が角度方向にずれていると、そこでは月の重力場が少し強くなっているためそれに引っ張られ始め、たとえ最初の時点では角速度が完全に等しくて(ラグランジュ点からみて)相対的に静止していたとしても、小天体はやがてその力によって動き出してしまい、角速度や高度が全部変わってきてしまうのである。
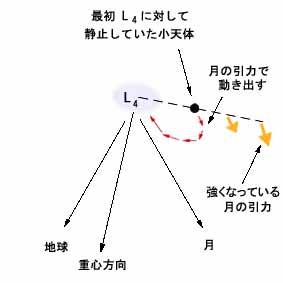
また図とは逆に、小天体が前方の位置に出過ぎていた場合も同様で、ここでは逆に月の引力は弱くなるので、小天体は次第に相対的に加速されていってしまうことになる。(なお余計なことかもしれないが一応つけ加えておくと、ラグランジュ点の位置からみた場合、この減速と加速の力はちょうど月による潮汐力がそこに働いているのと全く同じことである。)
このようにラグランジュ点の場合、単なる位置だけのずれといえども、それは間もなく角速度のずれを発生し、やはり一連の過程をスタートさせてしまうのである。これは表現を換えれば、ラグランジュ点は少しだけ離れた位置にあって(最初は相対的に静止していた)小天体を、むしろ能動的に動かして自分の中に引き込んでいく力をもっているのだと見ることもできるだろう。
以上のようにして、あたかも特殊な海流が浮遊物をそこに集めてしまうように、ラグランジュ点は近くの小天体をその周囲に集めてしまうというわけである。
さて以上でラグランジュ点の謎、すなわち釣り合い・復元力・質量制限の三点に関して、その大まかなメカニズムは、ほぼ直観的な理解ができたのではないかと思う。
なおあらためて注意しておくが、あくまでも以上の議論は、主要な要素だけを強調して多少デフォルメした「直観的方法」に過ぎない。
しかしながら前にも述べたように、一般に釣り合いの問題というのは厳密に言えば、極めて多数の要素が同格の立場で作用した結果生じた平衡点の話に過ぎないわけだから、それらすべてを厳密にもれなく扱うと、しばしばイメージそのものが根本的に失われてしまう場合がある。
これではもう人間の頭がそれを「理解」する意味が最初から存在しないわけで、ある程度のデフォルメはどうしてもやむを得ないのである。その点はどうかご了承されたい。
| Pathfinder Physics Team |