これから述べることは、恐らくこれまでこのサイトに掲載された文の中で最も重要なものの一つではないかと思われます。
実際に、以下の中には理系の世界に生きる人々にとって、かなり衝撃的な新事実が含まれていると思われ、中にはこれによって物事の認識が昨日とは違ったものになってしまうという方もあるかもしれません。
しかしながらその結論自体は非常に簡単に表現できるもので、そのシンプルさ故に応用面でも恐らく極めて重要なものになると予想されます。(そのため今これを知っていると、それだけでいろいろな分野で第一級の仕事ができるという可能性もあります。)
そこで、それが何かについて、以下に概略をダイジェストの形で記しておきましょう。読んで損になる話ではないことはとりあえず保証できると思いますので、是非目を通してみて下さい。(20030208 長沼伸一郎、20030304修正)
以下の内容の主題
その内容が何かと言えば、それは次のようなものです。つまり誰もが知っているように、一般に系というものは単純なものなら気軽にいじれますが、複雑でデリケートなものは、下手にいじると影響や副作用がどこに出てくるかわからず大変に危険です。
しかしそれならば、相互作用が具体的にどのぐらい複雑になると、危なくていじれなくなるのでしょうか。恐らくこの問いほど、現代の文明社会にとって切実に必要なものはないと言って良く、現実に周囲を見ても、例えば遺伝子解析の問題、医学、経済、環境問題など、様々な分野にとって今や待った無しの避けて通れない問題となっています。
そのためこの問に対して「人類はぎりぎりどこまでなら、その種の系をいじることが許されているのか」という答えを与えることは、現代の数学に課せられた最重要課題の一つと言って良いでしょう。
純粋に数学の問題としても、この臨界状態のメカニズムを解き明かすことは大変興味深く、やや大袈裟に言えばニュートン以後の数学が追うべき最大級の重要目標だったと言っても過言ではありません。しかしこれまで行われた挑戦はどれも泥沼化して結局みるべき成果を上げられず、現在ではほとんど断念されているのが現状です。
ところが作用マトリックス理論を用いたところ、その結果は意外にも自然対数eのからんだ形として、驚異的にクリヤーな形で出てきてしまったのです。
(なお「物理数学の直観的方法・第2版」をお読みでない方は、「作用マトリックス」とは要するに、系の各要素のもつ相互作用を特殊な行列の形で書き出したものだとお考えください。これはもともとは、三体問題が解けないことを最もクリヤーな形で示すために作られたツールでしたが、このような用途でも威力を発揮します。)
そして以下に示されるのがその結果です。つまり以下の内容は、具体的に系(およびそれを表現する作用マトリックス)がどのぐらい複雑になると、「いじれなくなる臨界点」に達するかという重要な問いへの、恐らく最もクリヤーと思われる結論です。
結論の要約
ではその結論を、本編に先立ってまず一足先に、ここでもう少しだけ詳しく紹介しておきましょう。その大略は次のようなものです。
それはまず、ある系が激変を起こしやすいか否かは、次の量に注目するだけで基本的に判定が可能になるということです。
その量とは、「系の内部で各要素が、他の要素に対して平均何個の相互作用を及ぼしているか」というものであり、その平均個数がある値を超えた時点で、系は一種の相転移を起こしてしまうというのが、第一の結論です。
要するにもし内部の相互作用の平均個数がその値以下ならば、その系はどこかをいじっても比較的安全ですが、それを超えた途端に、その系は過敏でいじれない性質のものに変貌してしまうのです。
そうなると次は当然、その具体的な値がいくつかということが関心事となってきますが、実はその結果こそが恐らくほどんど誰一人予想だにしなかったものでした。すなわちそれは、何と系のサイズに無関係にe=2.71・・個という値に定まっていたのです。
つまり一般的にどんなサイズの系においても、「相互作用の平均個数が自然対数e個」という状態が一つの臨界点となっていて、それを境に系の性質は全く異なるものに相転移を起こしてしまうという、驚くべき基本原理が存在していたというわけです。
そのため、ある系の性質が激変しやすい危険なものか安定なものかを判定したい場合、系のサイズを事実上気にすることなく、ただ単純に系内部の相互作用の平均個数の値を調べ、それがe個より大きいか小さいかを見るだけで、それを判定できるということになります。
およそこれ以上にシンプルで美しい結果というものは考えにくく、われわれ自身もその意外な結末に少なからず驚きを禁じ得ませんでした。
実際これがもしその通りなら、それは革命的なツールとしてこれまでの常識を塗り替えてしまう可能性を秘めていると言って良く、そのため今後この種の問題を扱うあらゆる研究・論文で、これが不可欠なツールとして登場してくることが予想されるというわけです。
では以下はいよいよその具体的内容のダイジェストです。
具体的内容のダイジェスト
(1)どうやってそのグラフを描くか
さてそんなわけで以下の中心課題は、要するにどうやって「系のデリケートさの臨界点」を表現するかということになるわけですが、その前に、そもそも何をもって「系が危なくていじれない状態」とするかを定めておかねばなりません。しかし作用マトリックスを用いるならば話は簡単で、それは要するに系の相互作用成分のどれか一つをいじった時、系全体に指数関数的激変が起こるか否かということで明確に定義できます。
(この話自体はすでに「物理数学・・」第二版の加筆部分、225ページ付近のオニヒトデと生態系の話などを通じて、定性的な形では議論がなされていました。)
そしてその種の激変が起こるかどうかは、結局のところ系の相互作用成分のどれかをいじった時に固有値(系の作用マトリックスの)が変化するか否かという問題に帰着し、そして一般に系が単純なもの−−つまり相互作用成分の多くがゼロ−−から次第に複雑化していくにしたがって、それが変化する確率がだんだん増していくということが、すでにわかっています。
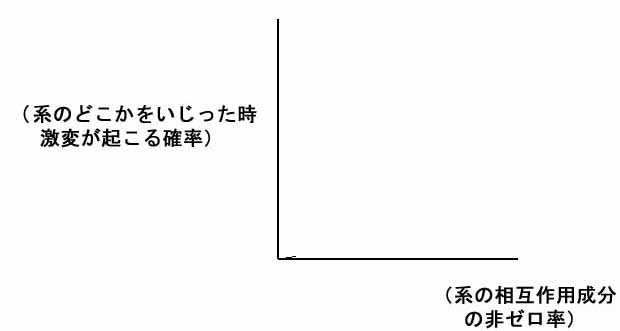
要するにその確率の増大過程をそのままグラフにしてしまえばよいわけで、そのためここではまず系の複雑さを表す指標として、作用マトリックスの相互作用成分のうちのどのぐらいが非ゼロ成分で埋まっているかに注目し、それを「相互作用成分の非ゼロ率」と定義して、それを0%から100%まで並べてグラフの横軸とします。
そして縦軸には言うまでもなく先ほどの確率、すなわちその系内部の相互作用成分を(どれでも良いから一つ)いじった時、系全体の固有値が変わってしまう確率はどの程度かという値をとります。
図1

このようにすればもうそれだけで、「どのぐらい相互作用のデリケートな系だといじって危険になるのか」の臨界点が定量的にわかる、凄いツールができることになります。(こんな簡単にそれができてしまうというのが作用マトリックス理論の威力で、従来の解析学を使ったら恐らく百ページぐらいではすまない分厚い代物になったでしょう。)
そしてそれを直観的に一発でわかるグラフとして描き出そうという試みが、この「臨界曲線」だというわけです。
(2)描き出された曲線
そしてそれを実際に行なって見た結果は、われわれの当初の予想を上回るものでした。まずこの「臨界曲線」そのものが、予想外に単純な関数で表現できることが判明し、手元のパソコンで数値解析が十分できる程度のものになってしまったのです。
これは、それまでその姿が謎であった重要な曲線を意味するため、われわれも重大な関心をもって、一体どのようなグラフが画面に現われてくるかを見守りました。そして画面上に描き出されてきたのは、次のようなS字型の曲線でした。
図2
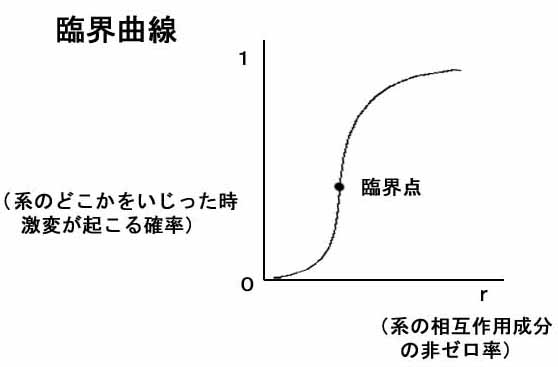
これが、これまで未知であった「臨界曲線」の姿です。そしてこれを見ると、最初のうち系の非ゼロ成分が非常に少ない間は、グラフの値は0のまま横ばい状態で安定な状態が続いているのですが、非ゼロ成分の割合がある時点に達したあたりで、値は急速に1にジャンプしていることがわかります。
つまりある一点を臨界点として、系の性質は鈍感なものから敏感なものへと急激に変貌し、危険でいじれないものになってしまっているというわけですが、ここで注意していただきたいのは、これが純粋に数学的に定まる基本的な結論であって、特定の物理的モデルなどを想定したものではなく、どんな問題に対しても共通で適用できるということです。
(この式の導出過程はそれほど難しくないので、腕に自信のある方はHP掲載の論文を追ってみると良いでしょう。詳細は第二支部掲載の「系が激変を起こす臨界点の定量的解析−−S,Naganuma,Rep.Path
Find.Phys.vol.1,pp24-34(2002)をご参照ください。)
(3)グラフの性質
この種の急激な変化というものは、現実にもいろいろな場所で見られるもので、そのメカニズムが比較的単純な式で表現できることがわかったというだけでも、ある意味で画期的なことでした。しかしそれ以上に魅力的なのは、その式をせいぜい大学初年度程度の数学で自由にいじることができて、その性質を解析的に調べることが可能になってしまったということです。そしてその結果判明したことは、もっと驚くべきものでした。
まずここで第一の興味となるのは、一般に系自体のサイズが大きくなっていくと、この曲線のパターンはどう変化していくのかということです。つまり例えば系の構成要素が10個から100個に増えていくと、曲線の形状は一体どう変わっていくのかということです。
その結果は、系のサイズが大きくなるほどその臨界点の値は小さくなって左に寄っていき、そして全体の形状はだんだん直角にシャープになっていくということがわかりました。つまり巨大な系の場合だと、内部の非ゼロ成分の割合がかなり僅かであっても、系全体は敏感に反応する性質をもつようになっているというわけです。
図3
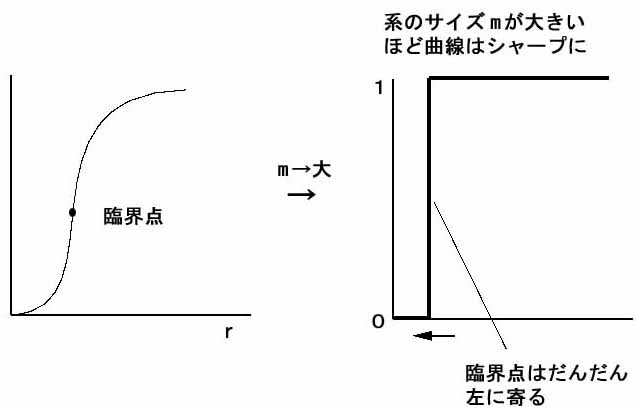
(これに関しては、系の構成要素20個あたりまでのグラフを描くソフトが論文の付録として掲載されていますので、動かしてみてください。)
(4)驚くべき結論−−現われたe
そうなると次の興味は、それが極限まで行って系のサイズが無限大になると、臨界点はどこに収束するかということですが、実はその結果こそ驚異的なものでした。
当初われわれは、グラフの上で臨界点がどんどん左へ移動していることからみて、解析的にも当然その結果はゼロに行くのではないかと予想していたのですが、結果はその予想を裏切るものでした。
実は何と神秘的なことに、それはゼロではなく自然対数eに収束していたのです。
もっともその結論にはワンクッション必要で、とりあえずの結論としては、系のサイズをm行m列とした時にそれはe/mという値に収束しており、そのため確かにサイズmが無限大に行くならば、一応その値はゼロに近づいていきます。
ところがここで注意すべきことは、もともとこの値は相互作用成分の中の非ゼロ成分の「割合」を示す数字だということです。そして一般にm行m列の作用マトリックスには、相互作用成分個数が1列当たりm個並んでおり、そのうちの何%が非ゼロ成分なのかというのがこの数字なのですから、1列あたりの非ゼロ成分の平均個数は、それにmをかけたものになります。
図4
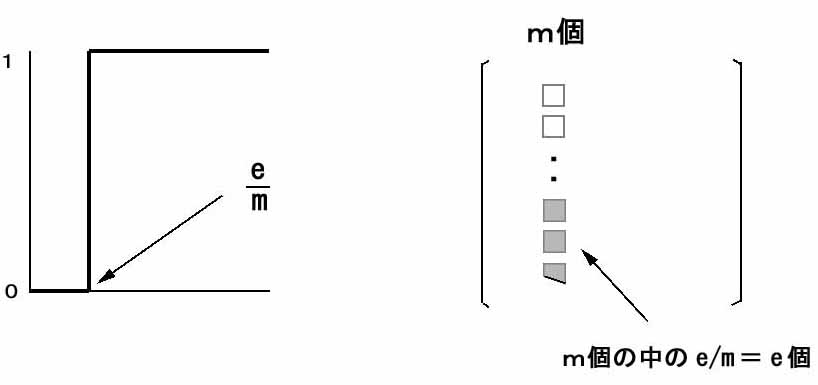
そのためその具体的な「個数」を求める際には、ちょうどe/mの分母のmがキャンセルしてeだけが残ることになり、mを無限大としても個数の値はゼロには行かず、eという一定値に収束するというわけですが、その意味たるや重大です。
それというのもこの個数というものは、臨界点(例の臨界曲線のグラフが垂直にジャンプする点)での条件を最も端的に示す数字だからであり、具体的に言うとこれは、そのとき系の内部の各要素がそれぞれ平均何個の相互作用成分をもっているか−−例えば医学の場合だと、ある一つの器官・組織が他の器官に対して平均何個の作用を及ぼしているか−−の個数を意味しています。
そして、系に臨界点をもたらすその個数は、何と系のサイズに無関係に一定値に定まり、さらにその一定値の正体はe=約2.7個そのものだったという、まことに驚くべき結果が出てきたというわけなのです。
図5
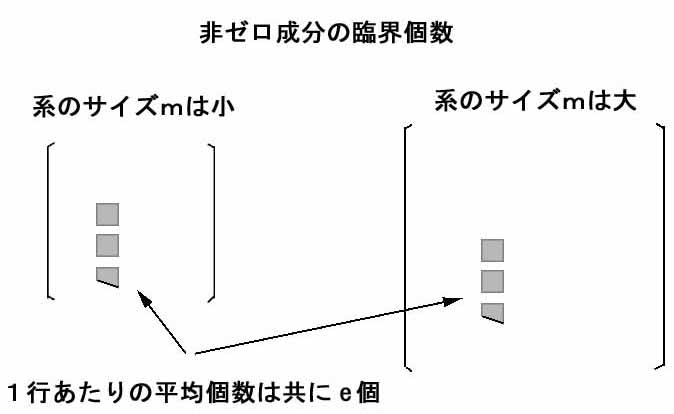
その結論の意味をもっと噛み砕いて言えば、それは次のようになります。つまり100個の要素から構成される系だろうと1000個から構成される系だろうと、その各要素が平均2.7個より多くの相互作用をもっているかどうかという一点のみに注目するだけで、その系をいじることが危険かどうかを基本的に判定できるということです。
すなわちそれが平均2.7個より多ければその系をいじるのは危険であり、逆にそれが平均2.7個より少なければいじっても比較的安全だということです。
ここまでシンプルな結果だとなれば、ツールとしての使い易さも抜群で、応用範囲がどれほど広いものになるかは容易に予想できるでしょう。
(この部分の詳細は第二支部掲載の「臨界点の定量解析とその応用」−−S,Naganuma,Rep.Path Find.Phis.,vol.1,pp.35-53(2002)をご参照ください。
なお念のため言っておくと、この結果は本来、ある程度以上に系のサイズが大きい場合に成り立つことです。もっとも実際に数値解析を行ってみると、それほど系のサイズが大きくない場合でも、その値は結構eに近い数値になっていることがわかります。数値解析の結果も載せてありますので、ご参照ください。)
本来ならこの種の問題は、三体問題以上に厄介な数学の暗黒領域にあって、これまで人類がほとんど手探り以上の認識を持ち得ない代物だったのですが、まさか事もあろうにそこにeが君臨していたなどとは、全く想像もしていなかったことでした。
ということは、今まで人類は周囲の現象の中でそこら中にeそのものの姿を、それと気づかず見ていたのだということになるわけで、何らかのシステム設計や解析に携わったことのある方なら、あるいは過去の経験で思い当たる例が何かあるのではないでしょうか。
実際これは哲学的・数学的トピックスとしても相当に衝撃的なものであり、次の世代においては理系全体ですでに不可欠な常識となっているという事態も十分予想されます。
応用の可能性
(1)遺伝子解析の危険度の判定
では具体的なツールとしてみたとき、どんな形で応用が考えられるでしょうか。まず第一に考えられるのが、遺伝子操作の危険度を判定するツールとしての用途です。
現在誰もが、遺伝子や生命という恐ろしく複雑でデリケートな系をいたずらにいじったことで、系全体が目茶苦茶な崩壊を起こす恐れはないのか懸念していますが、その崩壊の危険を数学的に解析するために使えるツールとしては、これは現在のところ最短距離にあると言えるでしょう。
要するに「要素1個あたりがもつ相互作用の平均個数」がわかればそれでよいというのですから、遺伝子という系を構成する要素のいくつかをサンプルとして選んで、それらが他の要素に及ぼしている相互作用成分の個数が平均2.7個以内に収まっているかどうかを調べればよく、それだけで一応の第一次テストが現実に可能になってしまうわけです。
(2)医学
また医学などにおいても、現在多くの人が、西洋医学的な手法の暴走や薬害の連鎖の拡大を身近な問題として切実に悩んでいますが、それこそがまさにここで言う「体という系のどこかをいじったことで生じる指数関数的迷走」そのものであり、それが起こるかどうかの鍵も、やはり臓器や組織などの間の相互作用の平均個数がe=2.7個より大きいか小さいかにあったわけです。
つまりその平均個数がいくつであるかは、医学そのものの根幹にかかわる問題であり、にもかかわらず現在の医学においては、いまだにその値が明確には知られていません。その意味では、これを知ることは今後の医学研究にとって最優先クラスの課題であると言えるでしょう。
(3)社会学・経済学
また、社会学などにおいても、例えば過去の経済史において、貨幣経済の急速な流入が伝統社会をあっという間に破壊してしまうという現象がありましたが、これなどは、誰もが即座にこれを用いて解析したくなる誘惑にかられることでしょう。その他の局面での応用の重要性も、言うまでもありません。
(なお、以上を見てもわかるように、この臨界曲線という話題に関しては応用分野が大変に広くなることが予想されるため、論文の記述に当たっては広い分野の方が抵抗なく読めるよう、読み易さという点を最優先に置き、数学的な過度な厳密さは敢えて第二優先としてあります。)
他の応用例についてはこれ以上列挙はしませんが、何しろ結論の衝撃度から考えると、到底応用がこの程度に留まるはずはなく、むしろほとんどあらゆる分野で、少なくとも一つぐらいは何か重要なものが眠っていると考えた方が良いでしょう。
われわれの側でも現在、周囲の分野などでそれを捜している最中で、現実に実測値データなどにおいて、個数e付近で顕著な変化が見られていると覚しきものが、いくつか見つかっており、もしそのうちのいくつかでも本物ならば、それだけでも大変なことになるはずです。(何しろ数学はここ百年ほど、この種の問題に対して使いものになるようなツールや結果を、ほとんど何一つ提供できなかったのですから。)
今、これを読まれている方へ
概要はほぼ次のようなものですが、では次にこれを読まれている方(そしてできればその内容の価値をお認めになった方)に、あらためて思いを致していただきたいことがあります。
それは、現在このことを知っている人間が何人ぐらいおり、そしてその人数が増えることがこの国に何をもたらすのかということです。
この場合、前者すなわち現時点でこれを知る人の数を推定することは比較的容易であり、要するに「物理数学の直観的方法」改訂第2版の読者数がそれに相当するわけですから、現在これを知りうる人の数は上限で約4000人というところでしょう。
ところがここにいささか特殊な状況が存在しており、それは「物理数学・・・」に関しては、第1版は読んだが改訂第2版は読んでいない、という人が相当にいるはずだということです。
つまりそれらの人々は、「物理数学・・・」そのものには馴染んでいるのですが、作用マトリックスについてはその存在をまだ知らず、しかしながらもし誰かに応用価値を一言聞かされさえすれば、即座に理解できる素地をもっているという人々です。
特に30代から40代の研究職にある方の場合、職場の周囲にそのような人々が相当に多くいるはずなのですが、問題はその人数です。
ここでまず、既に第1版の発行部数が3万数千部であることがわかっており、そして先ほどの4千人をそこから除いたものが問題の人数だということになりますから、差引き約3万がその人数で、そのかなりが研究所などに集中しているはずだということになります。ところが考えて見ると、これは実にとんでもない数字です。
つまり世界の技術大国の一角を占める日本で、その背骨をなす数十万人の科学者・技術者のうち、3万人が突然この「臨界個数がe」という事実を知るということを、ここで想像してみてください。
恐らくどこの業界でも、それが盲点となって進まなかった問題というものが一つや二つはあるはずで、それがこの人数のレベルで動きが始まるとなれば、その影響はあまりにも大きく、現時点でそれを全部予測することは困難でしょう。
しかしそのようなことを引き起こすために必要な行動というのは、考えてみるとあきれるほど単純で、要するに先ほどの4千人(第二版を読んでいる人)が周囲に潜在的に存在するその3万の人に一言この情報を何らかの形で伝えることができればそれで良いわけです。
つまり前者に属する人(無論今これをお読みの方も含まれます)が、職場などで何かの折に同僚にまず「物理数学・・」を読んだことがあるかどうかを尋ね、その際にもし「第1版だけは知っている」という答えが返ってきたならば、その時に話題として、作用マトリックスあるいはこのeの話のことを話せばよいわけです。
こうしたことがいろいろな場所で何気無く行われていけば、自然にこの数のギャップが埋まっていくはずであり、それだけで物事はゆっくりと確実に動いていくことでしょう。
思えば、これまで日本では末端の技術的なレベルで改良を行うような仕事なら自由にできましたが、もっと根本的な哲学そのものを左右する大きな仕事となると、とかく学会の頭部が動かないと胴体部分は動き出すことができず、そして日本では欧米のお墨付きがつかない限り頭部が動かないという処置なしの状況があって、常に戦略的に負けていくことを運命づけられていました。
しかしこのような形で物事を進められるとすれば、直接胴体部分が先に動き始めることになり、その構造に風穴が開く可能性が存在しています。実際問題、もしこのことを知る人数が3万に達するという事態に至ったならば、その既成事実の前ではもうお墨付きなどどうでも良いことで、どこかで何かが必ず起こるはずです。
この種の学問においてこういう機会が生まれるというのは、国にとってかなり稀なことであると言えるでしょう。そしてもし日本独自の動きが可能になるというなら、このさい失敗した米国の複雑系とは完全に袂を分かち、将来的には「日本では三体問題から再出発して全く別個の体系を発展させたため、それが米国の複雑系には不可能だった認識や発見への到達を可能にした」という魅力的なストーリーで、日本発のオリジナルな発展の物語を皆で作って未来に残していきたいものです。
それゆえ、具体的には
(1)ご自身の分野でこれが適用できるものが何かないかを調べること。
(2)この事実を先ほどの3万の人々に対して伝えること。
の2点について、ご協力いただければ幸いです。
それはともかく、従来この種の問題は、余りにややこしくて現代に至るまで数学的にはほとんど歯が立たず、現在でもただ無意味にコンピューターをぶん回してわけのわからないグラフを描き出す以外に、何もできていないというのが実情です。
ところがこれを用いると、まさにそれらの問題をちょうど18世紀の数学者たちのように「自分の手で直接いじれる」という感覚を味わうことができるのであり、それは19世紀以降、数学者たちが長らく忘れていた感覚であると言えるでしょう。
(なおそれほどの難物が、どうしてこんな驚異的な薄い枚数の論文でクリヤーに表現できるのかについては、第二支部に「難題の裏の意外なシンプルさの不思議」という文を掲載して、その背後に隠された歴史的な事情について述べる予定ですので、興味がおありの方はそちらもご参照ください。)
ともあれそんなわけで、数学を一度でも面白いと思ったことがおありの方にとっては、今これに触れてみることは(それを知る人数がまだ僅かであるという事実と相俟って)、実に得難い経験をすることになるものと思われます。