２－２ 人間側の直観力による反転攻勢
さて先ほどの２－１では、４つほどの状況証拠を示して、それを基に人間の直観力のメカニズムがどんなものかを推理してみた。そこで以下の２－２ではそこから一つ駒を進めていよいよ本書の最大の主題、つまりそのように想定した人間の直観力の最良のものが無限に発達した人工知能と対決したとき、果たして勝てるかどうかを数学的に立証するということを行うことにする。
ただし先ほどの４つの状況証拠だけでは、まだその決め手になるような性質が不足である。そのためここでは、この核心的な問題において鍵となる状況証拠を、さらに二つほど追加提示することをお許し願いたい。
そこで早速、そのうちの一つを紹介することにするが、その理由などの説明は後で行うとして、まず先にその内容を示してしまおう。それは、
状況証拠５・人間の天才の直観力は多くの場合、最初に最も重要な本質的条件だけをピックアップして全体の構図を決め、そこから下りていく形で細部を決めていく。そのいわば「上流から下流へ」の流れの中では、思考や手間の「逆流」は基本的には起こらない。
ということである。これだけではまだぴんと来ない方が多いと思うので、もう少し詳しく説明してみよう。
この話では「手間の逆流がない」という部分が特に重要である。作曲などの例で言うと、凡庸な作曲家の場合、まず最初に曲全体の大まかなイメージを据えるのは良いのだが、そこから下流へ向かって曲の細部を整えていくと、以前に定めた全体のイメージに手を加える必要が出てきてしまう。そうなると作業は最初に遡ってやり直しになり、これを何度も繰り返して、全体と細部の間で行ったり来たりの迷走を繰り返した挙句、作品が作れないということがしばしば見られる。
つまりこれが、下流から上流への手間の逆流が起こってしまっているということだが、実はむしろそれに陥ることの方が普通なのである。逆に言えばこれはそう簡単に誰にでもできることではなかったのであり、そして実はこれは人工知能で真似ることも思いのほか難しいのである。
つまりこの一見簡単なことを人間の直観力がちゃんと行っていたとすれば、それは重要な状況証拠の一つだと言える。そして後に見るように、それは数学的には大変な結果をもたらすことになり、人間が人工知能に反転攻勢に出る際に決定的な鍵となるのである。
人間の直観力の基本的なメカニズム
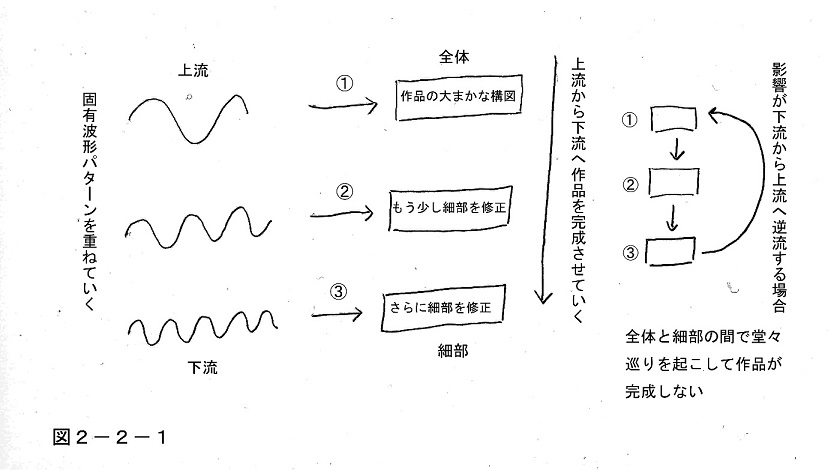
ではあらためてそれをもう少し詳しく見ていこう。この「上流から下流へ」という話は、２－１で述べた人間の直観力のメカニズムの中で考えるとよくわかる。その話を振り返ってみると、まず人間の頭の中にはもともと固有波形パターンのようなものがあって、何かを見たり聞いたりしたときにそれらがピーンと頭の中で共鳴するように立ち上がる。
そしてこれが大まかなものから細かいものまで何個か用意され、作品などを作ったりする際には、それらを頭の中で順次重ねていくことで作業を進めていくのである。
作曲などの場合で言うと、まず全体の構想が一つのビジョンとして頭に閃き、作品の大枠がそれで決定される。次の図ではこれが一番長い波形の①に相当し、それが一番上流に位置している。
そしてもっと細かい細部を詰めるため、②や③など、もっと細かい波形パターンをそこに重ねて、どんどん下流に向かって細部を完成させていくわけだが、ところがもしここで下流から上流へ逆流する形で影響が及ぶようになっていると、そういうことができない。
その場合には、細部を詰めるために②や③などの作業を行っていく過程で、全体に修正を加える必要が出てきてしまい、右図のように上流の①に立ち戻ってそこで作業をやり直さねばならなくなる。そうなると、優柔不断の堂々巡りのように全体と細部の間で行ったり来たりを繰り返して、到底作品を完成させるどころではなくなってしまうのである。
またこれは戦略の場合についてはもっと言えることで、優れた戦略家はまず全体の状況を見て、大まかに基本戦略を確定し、細部はその後で詰めて行く。場合によっては自分はその基本戦略の一番大切な点だけを決めるだけで、それを決めてしまった後は、残りの細部の策定は部下の参謀に下請けを出して任せてしまうこともしばしばある。
この場合、その大まかな基本戦略が一番上流の①に相当するが、多くの場合この段階で、戦局を左右する最も本質的で重要なポイントはすでにピックアップされているのである。そして②や③などに相当する細部が、二義的なものとして部下の参謀に下請けに出されるわけだが、こういう場合、若い未熟な参謀から見ると、どの部分が本質でどこから先は下請けを出せるのかを判断することができない。
つまり優れた戦略家の場合、その頭の中の固有波形パターンは、上流から下流に向かってきれいに並んで、逆流することがないような形で用意されていることになる。逆に言えば、そのように逆流を起こさないというのは、それ自体が優れた戦略家のみが持ちえる資質だったと言えるのであり、要するに「状況証拠５」の意味はそういうことである。
これはこの議論全体で鍵となる重要なことで、特にこれは後に述べる状況証拠「６」と一緒になると、人工知能では容易に真似ができなくなるのである。
物語文学や数学をどう波形で表現するか
さて一番重要な鍵となる話を一足先にいきなり述べてしまったので、基本部分の説明が後回しの格好になってしまったようである。そしてその基本部分の説明に関しては、以前の２－１でも十分に説明しきれていない部分が残っていたので、ここであらためて出発点に戻ってそれらを最初から述べていくことにしよう。
まず上の話のように、作品などを固有波形パターンの組み合わせで作るという話は、音楽の場合なら（最終的な作品そのものが「音」という波形で表現されていることもあって）それなりにイメージしやすい。
しかし文学や数学などの創作・知的活動の場合、その最終的な作品などは必ずしも波をイメージさせるものではないので、そもそもその「波形」が一体何を意味するのかが今一つぴんと来なかった、という読者もあるかもしれない。これは結構根本的な疑問かもしれないので、まず本題以前の話として、「物語などの起伏をどうやって波形で表現するか」という、基本的な話について少し見ておこう。
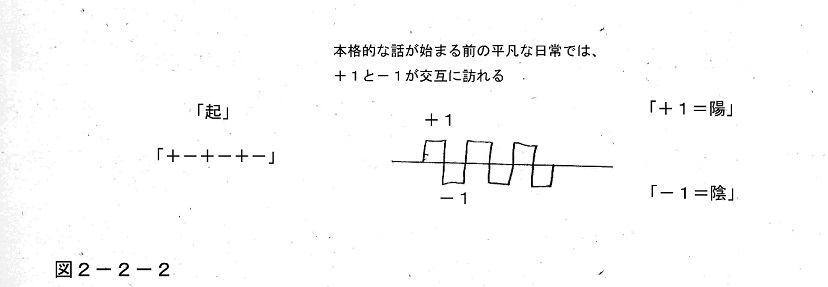
そこで話を思い切り簡略化するため、ここではひとまずそれらの起伏が単純に「＋１」と「－１」で表現されると考える。つまり物語の筋立てなどを表現する場合、平和で希望に満ちた状態を「＋（＝陽）」、困った事件が起こって不安な状態を「－（＝陰）」で表すことにして、それを左から右へ並べていくことで、物語が時間的にどういう起伏で進行するかを表現するのである。
そして昔から世の中では、物語の構成や四コマ漫画などは「起承転結」で構成される、ということが良く言われるが、ここでもそれに倣って、まず第一段階としてこの「起」や「承」などを、それぞれ個別にこういう＋と－で表現することを考えてみよう。
例えば最初の「起」だが、一般的な物語の場合、「起」では大体は事件が始まる前の平凡な日常状態が描かれるのが普通なので、そういう平凡な日常状態では＋と－が小さく交互に訪れる、という形で考えれば、その起伏は「＋－＋－＋－」という形になるだろう。
また次の「承」では、最初は平穏だったのに後半で予想外の困った事件に巻き込まれて、その起伏が「＋－＋－－－」の形となると考えられる。さらに次の「転」の部分では、希望が見えてきてそれが後半で本格化するので「＋－－＋＋＋」、そして最後の「結」で「－＋－＋＋＋」のハッピーエンドで物語がしめくくられる、という形で、それぞれの標準的な形が定まるわけである。
そしてこれらを左から右へつなげると、起承転結４つの部分の内部が、各６個の区画でそのように表現されているため、全体としては２４個の区画の＋と－でこの物語の起伏が表現される、というわけである。
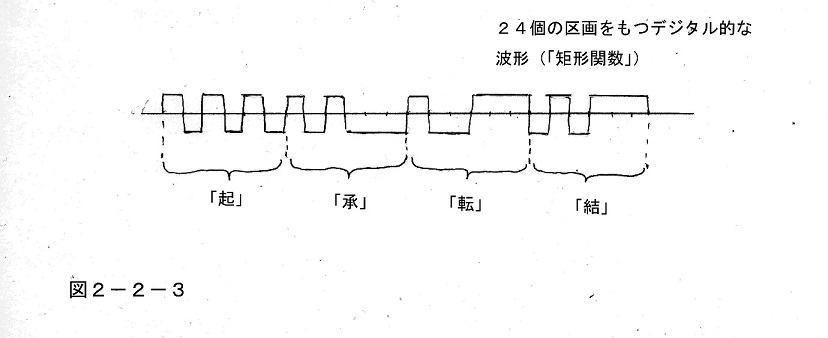
これは図に描いてみると、何だか一種のデジタル的な波形を連想させ、実際にこれは＋１と－１の値をとるいわゆる「矩形関数」の波に良く似ている。
そしてもっと長い長編小説などの場合も、この拡大発展版として考えることができる。つまり物語の大筋はこの起承転結の４つで基本線が定まるが、起承転結の４つの各部分をさらに細かく区分けして、それを入れ子式にどんどん細かくしていくことで、より巧妙な物語にしていく、と考えると、まさに物語の創造が、こういう波形イメージで表現しうる、ということになる。
さらに、今の話ではこの波形は単純に＋１と－１の二つの値をとるだけだったが、これをもう一段拡張して、物語の起伏の大小に応じて「＋５」や「－２」などいろいろな値を自在にとる形にすると、より本格的な表現が可能になる。
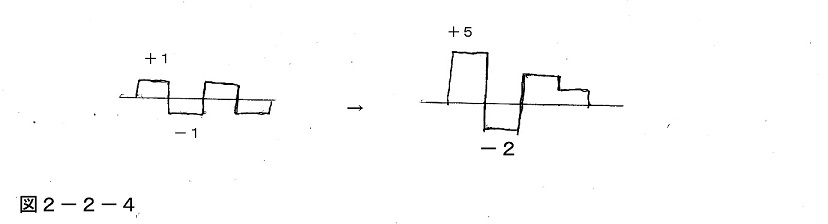
このように一般化すれば、交響曲の４つの楽章の盛り上がり方などもこういう形で考えることができるだろうし、一方美術や絵画などの場合はもっと単純に、上の話の「左から右へ」を時間経過ではなく、より直接的に「絵の構図の左側と右側」と考えればよい。
また数学や物理の場合だと、例えば物事をクリヤーに単純化して式がきれいになることを「＋」、いろいろなことを追加的に考慮して式が複雑化してしまうことを「－」と考える。
つまり一般に答えにたどり着くためにたどる経路は、大抵は途中で問題が複雑化して、一旦は混迷した「－」の状態に陥るものだが、絶妙な解き方をした時には最後にその式が一挙にきれいになって答えが求まり、それは一種のカタルシスを伴った「＋」の状態になる。それはちょうど交響曲が、途中で不協和音を拡大させながら、終曲の最後の和音で「＋」のカタルシスが鳴り響くのに似ているのである。
これは戦略の場合などでも似たような話が成り立ち、そういう形で考えるなら、音楽や数学物理、戦略などに共通する「美しいパターン」がこれによって表現できる、と考えることも十分可能だろう。要するにこれらのイメージを併せると、物語に限らず世の中の多くの創造活動がこうした一種の波形パターンで表現することができるという、この議論全体の前提をご理解いただけることと思う。
波形の重ね合わせで表現する
ではここまではご納得いただけたと思うので、話を先へ進めよう。われわれの直観力モデルでは次のステップとして重要になるのが、そのような形で音楽や数学を表現する波形が与えられた時、一般にそれはいくつかの基本的な波形に分解して、その重ね合わせで表現できるということである。
しかし実はこれも、先ほどのようにデジタル的な「矩形関数」で考えると非常にわかりやすい。例えばここで次の図のような波形があったとき、それは①～④の４つの重ね合わせで表現される格好になっているのであり、これは図からも簡単に確かめることができる。
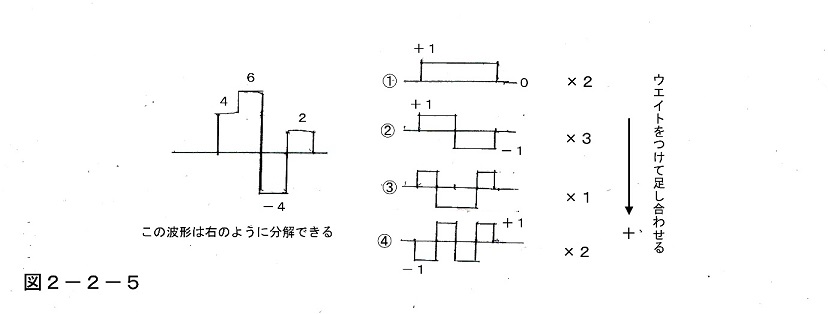
つまり図の中のオリジナルの波形は、これを①～④のような単純な波形に分解して、それぞれにウエイトをつけて①×２、②×３、③×１、④×２という形で足し合わせてやると、この波形を表現できるのであり、これはやってみればすぐわかるだろう。
そしてこの①～④が、以前から述べている「固有波形パターン」のイメージなのであり、人間の頭の中にはこのようなものが何個か用意されていて、優先順位をつけられて上流から下流へと並べられていると考えるのである。
なおこの場合、①から④に向かって、波形がどんどん細かくなっているが、これが「大まかな全体像から細部へ」の話に相当している。
そして物事を認識したり創作活動を行ったりする際には、先ほども述べたようにまず一番上流のステージで、目の前に与えられている問題（の波形）と、頭の中にある①の固有波形との共鳴度合いがチェックされ、それによってウエイトの大きさなどが決められて、まず全体の構図が定まる。
次にそれを除外した残りの部分をもって、一段下流の２番目のステージに進み、そこで②の固有波形で同じことが行われて、細部が順に決定されていくわけである。
これらの状況に最も適合する数学ツールは何か＝フーリエ級数
そしてこれを、＋と－だけのデジタル的な「矩形関数」のかわりに、もっと滑らかな波型の連続関数を使って完全な形にしたものが、「フーリエ級数」である。
現実にもそのように、複雑な波形パターンをいくつかの単純な基本波形パターンに分解して表現することは（以前に２－１でも述べたように）、物理的にも可能で、それはいろいろな場所で応用されている。例えば科学捜査の音声分析などで、オッシロスコープ上に映っている一見複雑な音声信号を、各周波数ごとの単純な波に分解して調べる、などというものはそれである。
その場合のデータは「何Hzの音が何％含まれる」などという形で表現されるが、この場合の各周波数の波が先ほどの①～④などに相当し、「何％」という部分が先ほどの「×３」などのウエイトの部分に相当する。
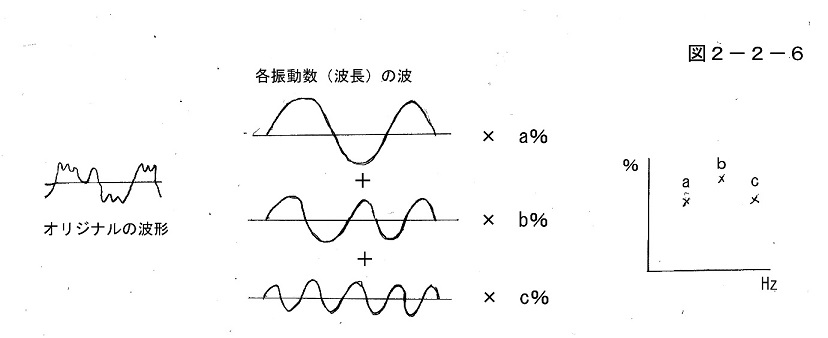
また光をスペクトルに分解して表現するのもこれと同じで、この場合にはその分解はもっと細かく連続的になっていて、それら各波長の分布グラフは滑らかな曲線の「スペクトル・グラフ」で描かれる。そのためその各波長の分布を示すスペクトルのグラフが与えられていれば、逆にそれを用いてオリジナルの波形グラフを完全に再現することができる。
その意味で、そのスペクトルのグラフとオリジナルの波形グラフは情報として等価で、どちらを使っても相手を完全に表現できる。そしてフーリエ級数とは、要するにこのことを完全に数学で表現したものだと思えばよい。
そのため読者は、上のことまでを理解できていれば、別に難しいフーリエ級数の話など理解する必要はなく、以下の話のためには十分な最低限の知識は得ていると思ってよい。
ただそれが数学的に定式化されていることで、われわれはそこでの法則などをそのまま使うことが可能となり、またそういう数学が存在するという事実そのものが、われわれにいくつか哲学的に重要なことを教えてくれるので、それらをいくつか列挙しておこう。
まず何といっても大きいのは、先ほども述べたように、とにかくこれを使えばこの世界に存在するあらゆる関数の曲線を表現できる、という点である。
そもそも数学や物理に基づく近代合理主義の一つの世界観として「この世の全ては関数で表現できる」ということが一つの基本思想となっている。ところがそのあらゆる関数が、フーリエ級数を使ってそのように表現できてしまう、というのだから、それは人間の頭脳が扱う全ての事象がやはりこの形で表現できてしまうということを意味していると言える。
つまりそれは言葉を換えれば、人間の頭脳活動のメカニズムを、そっくりこの方式に入れ替えてしまうことも、その気になれば十分可能だということであり、このツールが存在することで、それが完全に可能であるということが数学的に保証されていることになる。
またフーリエ級数からわかる重要なことをもう一つ挙げておくと、フーリエ級数の体系によれば、用意しておくべき基本波形パターンのワンセットは必ずしも一通りだけに定まっているわけではなく、ある程度の条件さえ満たしていれば、別の基本波形パターンのワンセットも考えることができて、そちらを使ってもよい、という法則が存在することが知られている。
これは、われわれにとっては意味の大きなことで、それは人間の頭の中にあると考えられる固有波形パターンが、個人個人で別のものであっても差し支えない、ということを意味しているからである。
そして扱う問題によっては、そのワンセットの良し悪しが、特定のパターンの曲線を大まかに描き出す際の実力差となって現れることがある。確かにあらゆるランダムな波形をどれも完全に正確に描き出すには、どのみち無限個の波形を用意してそれらを全部重ね合わせなければならず、その平均的な手間は、どのワンセットを使っても同じである。
しかし例えばもし、この世界の重要な問題の多くが何か不思議な共通性によって、どれも同じようなパターンをもっており、大事なものがその特定のパターンに集中していて、人間はそれさえ描き出せれば素晴らしい創作活動がいくつもできる、とすればどうだろう。
この場合には、その特定の形状パターンに特に適したワンセットを用意しておけば、僅か数個を重ね合わせるだけでそれらをかなり正確に描き出せる一方、他のワンセットを使ったのでは、数十個を重ね合わせなければそこまで似せられない、ということが起こり得るのである。
そのためこれを発展させると、万人に一人、自然界の調和や美と深く結びついた優秀な固有パターンを持っている人は、その４つか５つの組み合わせだけでも素晴らしい作品の大まかなイメージを得ることができる、ということになり、そういう可能性の存在が数学的に保証されているわけである。
具体的ないくつかのバリエーション
実際こういうものが現実に存在することによって、先ほどのように固有波形パターンを上流から下流に重ねていく直観力モデルをちゃんと作れることが、数学的に保証されることになるのである。
そしてその際に、優れた創作活動ではそれが上流から下流に整然と並んで、逆流を起こさない形になっている、というのが冒頭の状況証拠「５」の内容だったわけである。
こうしてみると、この直観力モデルは従来の演繹的な論理回路型のモデルとはかなり違っているが、しかしわれわれは必ずしも従来のモデルを完全に捨て去る必要はないかもしれない。
それというのも、われわれの直観力モデルは、全体の形をまず大まかに捉えて、徐々にそれを正確な値に近づけていくため、全体の把握は素早いが、逆に各部の正確な値を迅速に求めることは不得手である。むしろその点では、従来の関数的な方法論に基づく形の、演繹的な論理回路を使ったモデルやコンピューター・シミュレーションの方が優れており、こちらは細部の正確な値が先に求まって、最後に全体の形がわかる格好になることが多い。
つまり両者は一長一短で、むしろ互いに補い合うことを考えた方がよいのではあるまいか。つまりこれらが並立して「論理脳」と「直観脳」（これらは少し前までは「左脳」「右脳」と呼ぶのが常識だったが、最近では右脳と左脳の役割分担にはかなり疑問符がつけられているようなので、ここではそういう言葉を使った）のように互いに補完する形にすれば、それが最も望ましく、あるいは将来的にもそういうビジョンに落ち着くかもしれない。
ところでわれわれの直観力モデルの場合、人間の頭の中の固有波形パターンが具体的にどういう形で用意されているかは、その発展型のバリエーションとして、それぞれ異なった得意技をもついくつかのモデルを考えることができるので、参考までに記しておこう。
例えば「正解にたどり着く経路を直観的に素早く見つける」ことに有利なモデルとしては、次のようなものを考えてもよい。それは、各ステージごとに何通りかの異なる固有波形パターンが用意されていて、その中で最も強く共鳴したものが各ステージで選択され、それらを上流から下流へつなげていくことで正解の経路が描かれていく、という形のものである。
つまりこの場合には頭の中に一種の選択肢が用意されていて、各ステージで最適の固有波形パターンを選択して次々に先へ進んでいくことで、全体から細部へ向かう正解の経路が描かれていくわけである。
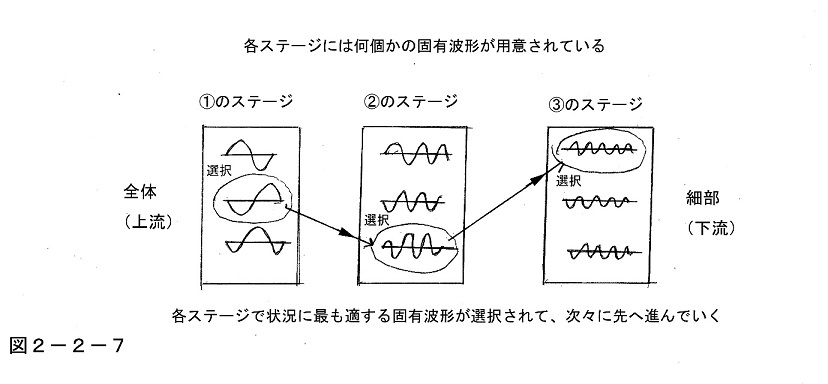
例えば戦略の問題の場合、頭の中にこれがあれば、局面全体で何が最優先かを迅速正確に探り当てて、優先順位を割り振って下請けを出すことも容易にできるだろう。そのように、これは「問題を直観的に解いていく」過程を説明するには向いたモデルである。
またこれとは別のもう少し違うバリエーションとして、「細部の作業をパートごとに分けて別々に扱う」ことに適した形のモデルも考えることができる。このモデルでは、一番上流の①のステージで全体を大まかに定めた後、次の下流の②のステージでは全体を右半分と左半分のパートに分けて、それぞれパートごとに細部を整える作業を行う形になっている。
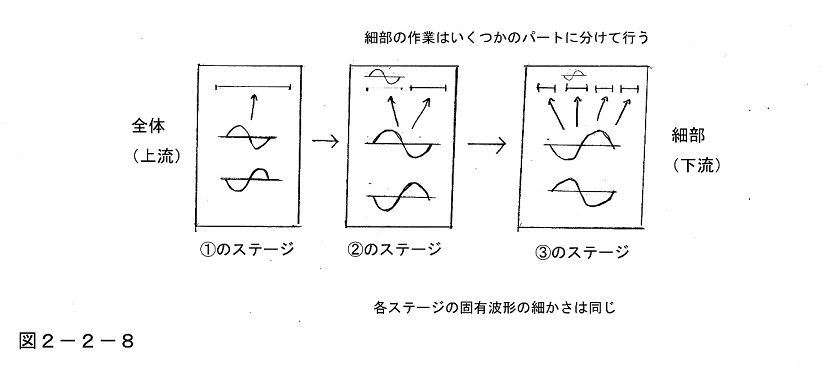
先ほどまでのモデルだと、下流のステージに向かうほど、そこで用意されている固有波形は細かくなり、またその細かさに比例して各波がもつ山や谷の個数も多くなっていた。しかしここでは作業内容自体をどんどんパートに分割して小さく短くしていくので、どのステージでも、用意されている固有波形の山や谷の数はほぼ同じものが使われる。
こういう形にしておくと、人間側は全体と細部のいずれの作業でも、それらを適当にスケール変換して同じ感覚で扱うことができ、現実の人間の創作活動もどちらかといえばそれに近い（ただしこういうパート分割が可能であるためには、前提として後の図２－２－９のようなことが満たされている必要がある）。読者は今後局面に合わせて、これらのモデルをいろいろ組み合わせていくとよいだろう。
もう一つの状況証拠＝その段階で組み込まれている「神は細部に宿る」の特性
さてそれはともかく、そのようなメカニズムを考えると、人間の直観力による創造活動をかなり良く表現できるというわけだが、現実の人間の活動を見ていると、ここでさらにもう一つ、人間の直観力には上等な性質が加わっていると想像されるのである。
よく推理小説で名探偵が、最初に事件現場を訪れた時に、周囲の人が誰も注意を払わないような細かいことにたった一人で着目し、それが後で推理全体の鍵になることが判明する、というストーリーがある。
むしろこれは名探偵ものの定番パターンと言っても良いのだが、実際に科学の歴史ではそういうことが現実に見られている。つまりそういう場合、他の研究者が全く些細な点として無視しているポイントにたった一人が着目し、後にそれこそが新理論の最大の基盤であることが判明するのである。そしてそれ以降、これを一番上流に置く形で体系が再構築され、後続の研究者たちが二番目、三番目と、下流に向かって細部を詰めて行くのである。
また作曲の例で言えば、ある曲の中にはしばしば曲全体の要となるような重要な一音が存在することがある。つまりもしその一見細かい音符がそう設定されていないと、完成した曲を聞いたときに、曲全体のイメージががらりと変わってしまい、全然名曲ではなくなってしまうのである。ところが優れた作曲家の場合、最初に曲全体の大まかな構想がぼんやりと頭に浮かんだ時点で、すでにその重要な一音だけは最初のイメージの中で定まっている、ということが多いのである。
これは第１部で述べた「神は細部に宿る」の話に照らすとより一般化でき、こういう場合には細部に一見ミクロ的だが実は全体に巨大な影響を及ぼす要素というものが存在しているのだが、それは一番上流の①の段階ですでにピックアップされていて、その一番上流の固有波形パターンの中に組み込まれてしまっているということである。つまり整理すると
状況証拠６ 上のモデルで頭の中に用意されている優れた固有波形パターンの場合、その一番上流のステージにある波形には、すでに問題全体の重要な鍵となる「神の宿る細部」が組み込まれている。
ということである。これは後に眺めるように非常に高級な機能で、人工知能では容易に真似ることができないのだが、現実の人間の創造活動を見る限り、人間の優れた直観力にはしばしばこういう極めて上等な機能が備わっていると想像されるのである。
それが一番上流で組み込まれていないとどうなるか
実際そういう能力をもっていることは、先ほどのように作業を上流から下流に向かって整然と行う上で、むしろ不可欠なものと考えられるのである。
つまりそのように、まず一番上流の①のステージで大枠を定め、下流の②や③のステージで細部を作り込んでいく場合、もし「神が宿る細部」が存在しているとなると、話は厄介なことになる。例えば図のｃ点部分がそういう重要な一点なのだが、①のステージで全体の大枠を定める際には特にそれに気づいておらず、中図のように細部の話として後回しにしてしまったとしよう。
そしてもっと細部を決める③のステージあたりで、ようやくそこに着手するのだが、ここを下手にいじったことで全体に大きな影響が及んでしまうと、①に舞い戻って作業をやり直さなければならない。こうなると先ほどの凡庸な作曲家のように、細部と全体の間で堂々巡りの迷走ループを延々と繰り返した挙句、曲がいつまでも完成しないのである。
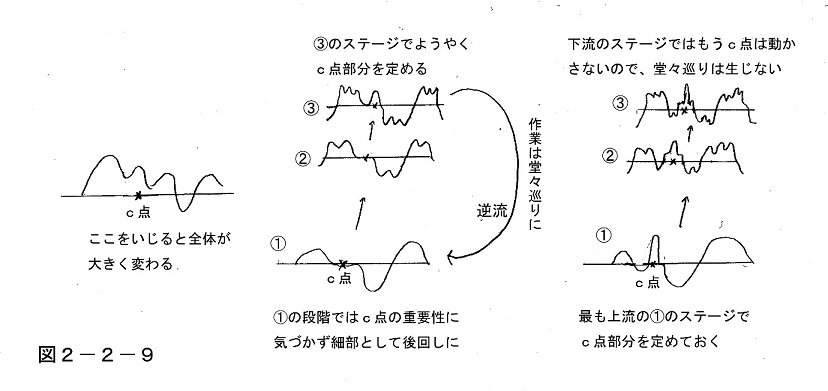
それを避けるためには、右図のように①のステージですでにそれをピックアップしておかねばならない。つまりその場合、①で用意されている固有波形では、その山の一つが例外的に、この細かいｃ点部分の極小の山だけのために専用で割り当てられており、とにかくそこが一番最初の段階で決められている。
そして①で表現しきれなかった残りの部分が、②と③で補足的に表現されていくが、その段階ではもうその微小部分には一切手をつけなくてもよい恰好になっているため、②や③のステージで何か修正を加えても、最初の①にその影響が及ぶことはない。
そのように、普通なら無視されて後回しにされるような細部が最初にピックアップされていれば、上流から下流へ向かう過程で、逆流による堂々巡りが起こらないことになり、人間の創造活動ではしばしばそういうことが行われていると考えられるのである。
ディラックの天才的直観力
そして過去にそういう例として最も顕著だったものが何かと言われたならば、筆者はその一つとして、人類が「反物質」を発見した時の例を挙げたい。これは人類文明史上のエポックだったと言えるが、彼がそれを発見した経緯がまさに上のようなものだったのである。
その詳細自体はここでの議論にさほど必要な話ではなく、また理解せずとも別に話の大筋には影響はないが、しかし具体的にそれがどんなものだったかを知りたい読者も多いと思うので、一つの科学史上のエピソードとして以下に紹介しておこう。
これは具体的には、量子力学が最初にスタートしてから20年ほどたった時に、英国の物理学者ディラックが粒子の「スピン」を発見した時の話で、それが同時に反物質の発見も意味していたのである。
その経緯について言うと、それまでの量子力学は、比較的ゆっくり動く粒子などを扱うように作られており、もっとスピードが速くて光速に近い速度で動く粒子を扱おうとすると、相対論の影響が現れてきてうまく出来なかった。しかしやはりそれでは駄目だというので、体系全体をアップデートすることが要求されてきた。
そこで世界中の物理学者たちがこの問題に取り組み、間もなく一応の解決にはたどり着く。そうやって見出された新しい方程式（「クライン・ゴルドン方程式」と呼ばれる）は、ちゃんと相対論に対応できるもので、数学的には完全なものだった。そして実験データと照合しても、少なくとも当時の水準からすれば十分に合格圏内にあり、要するにどこから見ても何の問題点もなかったのである。そのため当時の誰もが、この問題はもうこの新しい方程式で完全に解決したと考えていた。
ところが世界中の物理学者の中でほとんどただ一人、ディラックだけはそうは考えなかったのである。そして彼がその方程式を誤りと考えた理由は、論理的なものというよりはむしろ「この式を使うことは体系として美しくない」という美的・直観的なもので、彼はそれこそが最優先事項と考えて思考の一番上流に置いた。
しかしこれは客観的に見ると、当時としてはほとんどあり得ない選択だったのである。確かにその「クライン・ゴルドン方程式」をこの問題で使おうとすると、物理的解釈に強引なつぎはぎの部分が現れて、体系としてはきれいではなくなってしまう。しかし数学的に見る限りはどこも間違ってはおらず、実際にこの方程式は現在でも他のもっと小さい問題に対してなら十分使えるもので、要するに何一つ非の打ち所のないものだったのである。
そのためほとんどの物理学者が、これで問題解決と考えて、ディラックが気にしていることは優先順位の低い細部だと見なしており、むしろディラックの考えるきれいな体系に見合う式を見つけることの方が、遥かに難題だったと言える。
実際にディラックの求めるような体系の美しい式を見出すことは難しく、常識的な格好の式ではどうやってもそれができなかった。しかし彼はあくまでもその要求を優先し、式の格好自体を今までの常識ではまず使われなかった、一段階複雑なものに変更することで、ついにそれに成功する。
しかしこの「ディラック方程式」は、式の格好を一段複雑なものにしたため、本来なら一つだけ出てくるはずの答えが、＋と－の符合がついて２種類のものが出てきてしまった。（これはわかりにくければ中学高校の二次方程式の問題を思い出すとよい。そこではしばしば本命の答えと一緒に、マイナス符合がついた答えが出てきてしまうことがあり、特に応用問題の場合だと、それは答えが「リンゴの個数が－３個」などの無意味なものになることが多く、あるいは読者も中学高校の試験の時に、そちらを捨てて＋の方だけを解答欄に書き込んだ、という経験があるかもしれない。）
ところがここでディラックはさらに意外なことを主張した。つまり彼は、そういう負の量はこの美しい体系から自然に現れてくるものである以上、これは無意味な解ではなく、むしろ宇宙のどこかにそういう量が実在しているはずだ、と考えたのである。
そしてやがて驚くべき事実が判明する。つまりディラックの予言に従って探してみたところ、本当にそういうものが見つかってしまったのであり、それこそが「反物質」だったのである。これは人間が紙と鉛筆だけを使って、この宇宙にはわれわれが知っている物質とは正反対の性質をもつ「反物質」というものが存在する、という認識にたどり着いた人類史上の偉大な瞬間だった。
そして話が前後する格好になるが、そもそもこの式全体がいわゆる「粒子のスピン」も表現するものとなっており、結果的にその完全な表現が手に入ったのである。逆にもしディラックのこの認識がなければ、人類はクライン・ゴルドン方程式による誤った体系をベースに基本理論を作ってしまい、次々に現れる実験データとの齟齬をその都度、理論を複雑化することで強引に辻褄を合わせることを繰り返していたかもしれない。そしてその際にはニュートリノの発見などもどうなっていたかわからず、われわれは異常に肥大化・難解化した汚い理論体系を抱えたまま、今もそこから抜け出せていなかったかもしれないのである。
（注・なお物理が相当わかる人のために述べておくと、実はこのクライン・ゴルドン方程式は、シンメトリーという点では十分に「美しい」ものだった。しかし問題は、これをそれまでの量子力学の標準であった、比較的ゆっくり動く粒子を扱う場合の「シュレーディンガー方程式」と比べると、式の恰好が根本的に別物で、そのため扱う粒子の速度が上がっていくと、どこかで方程式の格好や体系を別物に切り換えねばならない、という解釈上の弱点があることだった。
これは確かに体系としてはつぎはぎ細工的で汚い。つまり曲に喩えて言えば、クライン・ゴルドン型の方は一個一個の和音だけは十分に美しいのだが、曲全体を通して聞くと構成がちぐはぐで全然美しくないのである。そのためディラックはむしろ曲全体の美しさという、一段上のセンスでそれを見ていたのだと言えるかもしれない。そして前者の美しさは簡単に模倣できるが後者の美しさは容易に真似できないのである。）
満たされていた二つの状況証拠
それはともかく、この事例をわれわれの観点から振り返ると、あらためて驚かされる。まずこの場合、「状況証拠５」はほぼ完全な形で満たされている。つまりこの場合、一番上流のステージで大枠を決めたのは、ディラックの「体系の姿はそんな汚い点を抱えていたのでは駄目で、こういう美しい姿であるべきだ」という直観的な信念である。これは一番上流に位置を占めたまま、現在に至るまでほとんど一度も修正されておらず、それは言葉を換えれば、下流から上流への逆流が全く起こらなかったということである。
そしてこれは当時、彼以外の誰もが注目していなかった盲点であり、その意味ではこの重要ポイントは一般には「無視して差し支えない細部」に分類されていたのだが、実はその細部は全体の結論に巨大な影響を及ぼすものだったのである。
そのためこの場合には、一番上流の段階ですでにその細部が選択されていたわけで、「状況証拠６」も満たされていたことになる。実はこれは想像以上に大変なことで、良く考えればわかるように、これはビッグデータをいくら駆使しても基本的にほとんど不可能なことなのである。
まずそもそもディラックが最重要ポイントとして選んだものが、一体他のいくつの候補の中から選ばれていたのか、ということからして問題である。読者にも経験があると思うが、一冊の本を読んでいて、重要だと思う場所にマーカーでアンダーラインを引いていくと、だんだんその箇所が増えて行って、結局本のほとんどがマーカーで埋まってしまう、ということがしばしば起こるものである。
つまりあらゆる注意ポイントを、そんな細部に至るまで前もって全て洗い出す、ということになると、分厚い量子力学の解説書まるごと１冊分についてそれを徹底的に行う必要があるため、マーカーの箇所は数千近くなり、結局それらを全て候補としてピックアップせねばならない。例えば比較的少なく見積もって、１ページあたり平均２か所のアンダーラインに絞った場合でも、500ページの量子力学の本では１千か所を超えることになる。
そしてその中から最重要なものを選び出すわけだが、ここでビッグデータを用いてそれを行おうとすると、どうしても有力な物理学者の意見を統計的に整理して、その最大公約数をとったものを最優先に選択する、という形態をとらざるを得ない。
そう考えると、その数千個の中で、ディラックが選んだものは恐らく優先順位の点で最下位クラスの「最も些細な点」として、効率的なデータ処理の観点からは真っ先に消えてしまっていたはずである。
またあらゆるパターンを虱潰しにするというアプローチをとる場合も、その困難は想像以上である。つまりもし先ほどのように「注意を払うべき細部」が潜在的に１千箇所あるとすれば、先ほどの図２－２－３のような波形パターンでそれをカバーするためには、山と谷の個数を１千個は用意して、その＋と－を考える必要がある。そうなればその全パターン数は２の１千乗ということになり、到底割り出せる代物ではなくなってしまう。
逆に言えばディラックはまさにそういうものを選んでいたわけで、そしてそこからさらに細部を詰めて、二番目、三番目と下流に向かってどんどん足し合わされる形で、次第に量子力学の具体的な細部が明らかになっていったわけである。
要するに人類が「反物質」というものの存在を発見したとき、その科学史上の偉大なステップにおいてまさにそのような構図で知的活動が行われていたわけで、これと比べると他の如何なる芸術作品の事例といえどもさすがに影が薄く、これを人類史上最大級の実例の一つと評することに異論はあるまい。
集団的に形成された上流からの流れ
またこの事例の場合、その上流から下流への流れは必ずしも一人の頭脳の中だけで完結していたわけでなく、彼の後継者となる複数の人間との間で共有される形で、ちゃんとその流れが作られたという点でも、極めて注目すべきものである。
先ほどの例を見ると、ディラックがこの結論を得た後、他の物理学者たちがそれを受け継ぐ形で、彼のインスピレーションをヒントにさらに四番目、五番目…と下流に向かって細部を詰めて行く格好になっていた。
つまりこれを見る限りでは、この上流から下流へ向かう構図は、必ずしも一個の頭脳の中だけで完結していたわけではなく、何人もの人間の間で全体として一つの大きなピラミッド型が構成されていたことになる。
そう言われてみれば、われわれは他の場所でもこれに似たことがしばしば起こっていることに気づくのであり、例えば名指揮者とオーケストラの間に生まれる不思議な関係というものも、これに似ているかもしれない。
つまり指揮者が何か楽曲解釈のインスピレーションを得て、それをオーケストラに指揮棒で伝えると、それを受け取ったコンサートマスター以下の各楽団員は、たとえ細かい具体的な指示までは与えられずとも、そのインスピレーションに触発されて指揮者が期待した以上の音を鳴らすようになることがある。
実際に極端な場合、不思議なことにその指揮者が指揮台に立つだけで、オーケストラはなぜか今まで出したことのない音を出せるのだが、指揮者が指揮台を降りてしまうと、もうその音を鳴らすことができず、各楽団員も自分たちがどうやってそういう音を鳴らしたのかわからないので、指揮者が台に立ってくれないと再現ができないというのである。
これなどは、直観力が複数の人間の間でピラミッド型に共有され、全体として大きな知的活動が行われている例として解釈できるのではあるまいか。
また戦略における軍の指揮形態の問題に関しても、理想的な統率とされるものがやはりこれに似ており、それに関しては後に第３部で述べるが、一番トップの人間の霊感が下位にある何人もの人間のそれを順に刺激して、全体があたかも一個の頭脳をもつように動くことがあり、近代以降の戦史でも現実にそうした事例をいくつか認めることができる。
ともあれ量子力学のこの部分はディラックの彼の後継者たちとの間でそのような構図で発展していき、彼がその最初の発見を行ってからそろそろ90年になるが、現在に至るもなお、ディラックが最初に描いた「方程式や体系はこういう美しい姿をしているべき」という直観的な洞察は、一番上流に位置を占めたまま、ほとんど一度も修正されることはなく、確固たる出発点として量子力学の体系を支え続けている。つまり下流から上流への逆流が事実上起こっていなかったわけで、これは良く考えると大変驚くべきことである。
これによって生まれる驚異的な数学的構図
そして人類の過去の偉大な知的活動を他にも振り返ってみると、実はその多くがこのように状況証拠「５」と「６」を満たす形で行われていたように思われる。ところがこれをきちんと数学的に眺めると、その意義が途方もなく大きなものだったことがわかってくるのである。
ここで読者は第１部で述べたことを思い出していただきたい。それは人間や人工知能の思考のプロセスを作用マトリックスで表現したとき、それがもし次の図のAのようなパターンになっていた場合には、問題の規模を拡大すると計算の手間が幾何級数的に増大してしまうが、Bのようなパターンの場合には算術級数的にしか増大しないということである。
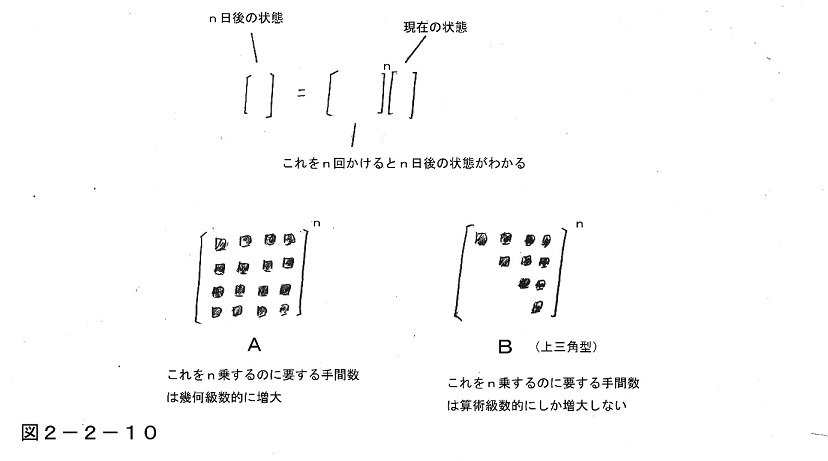
つまりAのパターンとBのパターンは質的に見ると根本的に別物になってしまっているのだが、実は先ほどの話で人間の天才的な直観力に見られていた、状況証拠「５」と「６」が満たされている（つまり逆流がない）状態というのは、作用マトリックスで表現すると、まさにBのようなパターンになるのである。
そしてこの意義が如何に大きなものであるかは、これと同じ構図が三体問題の時にも現れていて、それが「問題が解けるか否か」という重要な話に関連して「Aだと解けないがBだと解ける」という、哲学的に重大な話につながっていたことからも推察できる。
そこでその話をもう少し詳しく言うと、そもそもニュートンの時代でも特殊ケースとして、太陽の引力だけが非常に大きくて、各惑星の引力がそれに比べればほとんど無視できるような場合には、天体が何個でも例外的にちゃんと問題が解けていた。
実を言えばわれわれの世界史の19～20世紀にかけての驚異的発展は、こういう問題だけを解くことで可能になっていたとも言えるのだが、ところがこういう問題は、作用マトリックスで書くとBのパターンになっているのであり、物事をそういう形にできることの意義はそのように非常に大きいのである。
なおその場合になぜこのパターンになるかを一応簡単に示しておくと、一般に作用マトリックス内部では表記上の問題として、物事の影響が左回りの矢印で及んでいく格好になるので、図のように太陽を一番下の位置に配置すると、太陽から惑星への引力は行列内部の右上側に描かれる一方、各惑星から太陽への引力は左下側に描かれる。ところが後者はほぼゼロとして無視できることになっているので、左下部分がまるごと消えて、全体としては上三角行列のBのパターンとなるのである。
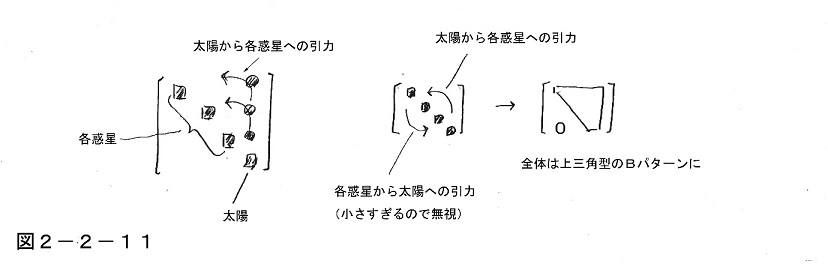
そしてそのようにBのパターンにできる場合、答えを求めるための手間数が可算無限個に収まるので、その問題は解くことができるが、こういう格好に直せないAの状態のままだと、答えを求めるための手間数がどうやっても非可算無限個になってしまうため、それは解くことができない、という壮大な哲学的な結論につながっていたのである。
なお今の太陽系の話では「各惑星の引力が太陽に比べて極度に小さくて無視できる」という、単純な大きさの差の話によってBのパターンが達成されていたが、人間の創作活動の場合には、むしろ「神の宿る細部」の有無が鍵を握ることとなる。
実際先ほども図２－２－９のところで述べたように、優れた創作活動の際にはそういう重要な細部が①のステージですでにピックアップされていると想定されており、次の左図でも示すように、①のステージでいろいろ修正作業を行うと②と③のステージも含めた下流全体にその影響が及ぶが、②と③のステージでどんな修正を加えてもその影響が逆流して①に及ぶことはない。
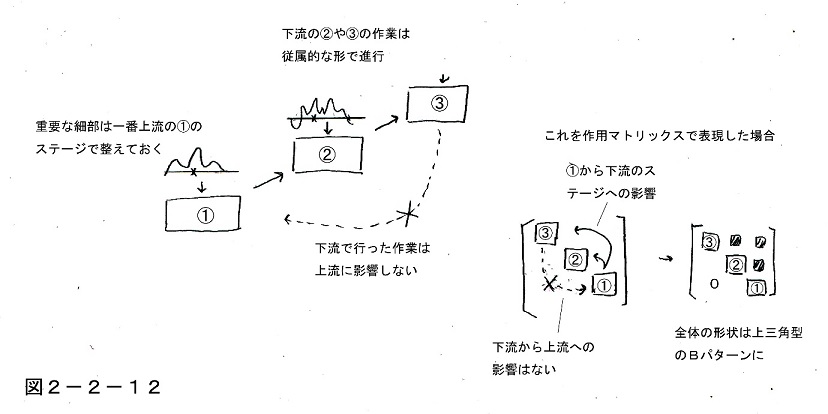
つまりこれを右図のように①の作業工程を先ほどの太陽の位置に置いて、作業工程同士の関係を同じような格好で表現した場合、②や③で修正を加えたことの影響は、各惑星からの引力が無視できるのと同様の構図でゼロとなるので、やはり全体がBのパターンになるわけである。
なおこの場合逆に言うと、もし後者のような「神の宿る細部」の部分が最初から存在せず、前者のように単純な量的な大小がそのまま重要度を反映している問題だけを扱うのであれば、人工知能でも比較的簡単にその機能を真似ることができる。
そういう場合、まずビッグデータから最も目立つ大きな山を探し出し、それらをピックアップすることで一番上流部分の基本パターンを定める。そして残った部分で再び同じことを繰り返し、それをどんどん下流に向かって続けていけば、大した困難なしにそれを真似て、上流から下流へ作業が一直線に流れる形を作ることができる（実を言うと教科書に載っている普通のフーリエ級数の場合も、基本的にそのような単純な問題が想定されているため、そういう要領で各波形を決定でき、またその際には特に作業の順序を気にする必要はない）。
ところがもし細部のどこかにそういう特殊な一点があると、先ほどのように堂々巡りに陥ってそれが全くできなくなる。そして現実の世の中の重要な物事は、実はむしろそういう問題の方が多いのである（それは第１部でも「初期値敏感性」という話題で論じていたので参照されたい）。
人工知能による追随の困難
なお読者の中には、一般に問題がたとえ最初の時点ではＡパターンのような格好で与えられていて駄目だったとしても、問題そのものの内部手順をうまく並べ替える作業などを人工知能の物量作戦に物を言わせる形で行っていけば、いずれはＢパターンのような上三角型に持っていくことができ、結局最後は人工知能はその弱点をカバーして十分に追随できるはずだ、と思っている方もあるかもしれない。
しかしもしそう考えていたならそれは錯覚で、実はそれは数学的には「三体問題などが原理的に紙と鉛筆では解けない」ということと同様の理由で不可能なのである。つまりこの場合もしそういう並べ替えができるなら、それらの問題も解けてしまう理屈になってしまうからである。
ところがそれが数学的に解けないことはそちらの方面ではすでに常識で、もし読者の頭の中で天体力学のビジョンと人工知能の話がつながっていれば、それが錯覚であることはすぐわかるはずである。ところが世の中ではまだ両者の話の接続が十分ではないため、そこが盲点になりがちであり、その観点からもこの両者の話題がつながることの意義は大きいと言えるだろう。
一方人間側について見てみると、そういう能力が一体どこから来るのかは、次の２－３でも「非線形問題の暗号」との関連で少し述べるが、われわれにとっては理屈よりも、むしろ現実の状況証拠として「５」と「６」が本当に成り立っているかどうかの方が重要である。つまりもしメカニズムが多少不明でも、現物がそこにあるというならこの議論は十分成り立つからである。
そこでそれをもう少し厳しく吟味すると、確かに人間はあらゆる問題についてこれができているわけではなく、最も優れた人物の場合でさえ、目の前の問題に対してせいぜい２割程度までを発揮するのが限度であり、本来なら証拠としての信頼性は十分とは言えないかもしれない。
しかし上の話が教える重要なことは、数学的にきちんと見ると、たとえ１割程度でもその効果は人工知能では到底真似ができないほど大変なものだということである。そして人間側の優位はもともとそういう一握りの突出した成果に依存していて、その期待値が問題になるので、効果の側が大きければ証拠の量自体は水準以下でも良いことになる。それならこれまでの人類の知的活動で見られた事例だけでも、量的には証拠としての必要ラインを十分クリアできるだろう。
つまりそういう数学的な保証と一緒に考える限り、一応は人間がそういう能力をもっていると結論して差し支えないというわけである。
人間の直観力がそういう能力をもつことの巨大な哲学的意義
とにかくこうしてみると、実は人間の直観力が状況証拠「５」と「６」を満たしているという、一見すると別にどうということはない能力は、想像以上に大変なものだったことがわかるだろう。
実際人間の直観力に（詳細は完全には不明だが）もしそういう能力が備わっているとするならば、そこに隠された意義は巨大である。つまりそれは先ほども述べたように、人間は難しい問題を直観力で比較的瞬時にBのパターンで近似して捉えることができるが、人工知能はAのパターンのまま、力任せに演算の物量作戦で行うしかない、ということである。
そしてこれは、作用マトリックスを使うと直ちに重大な結論に直結し、この状態のまま問題の規模を極限まで拡大していくと、人工知能のAのパターンでは演算の手間が非可算無限個になって、宇宙の終わりまでかかっても解けなくなってしまうが、人間の直観力のBのパターンならば、原理的に可算無限個の手間で解けてしまい、大まかに答えの格好を知るだけなら非常に迅速にできてしまう、というビジョンが浮かび上がってくるからである。
そして、AとBが質的に全く別物だという話を踏まえて、それをもう少し哲学的に拡大解釈すれば、人工知能と人間は「二つの無限」（つまり「数えられる無限＝可算無限個」と「数えられない無限＝非可算無限個」）の世界において、最初からこれらの異なる世界の住人だった、という一種壮大な思想に導かれるのである。（これはあるいは将来的に「人工知能が無限に発達すればいつか『意識』をもつようになるか」などの問題に影響を及ぼし、その観点からあらためて考え直すことが必要ではないか、という話に発展するかもしれない。）
ともあれ話を戻すと、人工知能側のAのパターンでは、問題の規模を拡大すると手間が幾何級数的に増大するのに対し、人間側の直観力のBのパターンでは算術級数的にしか増大しないのであり、これを応用することで、ついに人間側は人工知能に本格攻勢に転じることが可能になってくるのである。
人間側が反撃する際の最も有効な戦術
実際にこのことがわかったとなると、人間が人工知能に反撃を行う際には具体的にどんな戦術が最も有効かということが、数学の根本の理屈から自然に浮かび上がってくる。
そしてずばりその答えを言うと、この場合には先ほどもちょっと見たように、とにかく扱う問題の規模を拡大してしまえばよいのであり、そうすれば幾何級数的増大のメカニズムが効いてきて、人工知能を簡単に引き離してしまうことができるのである。
より具体的に言うと、その際には問題の中で考慮すべき要素の個数を増やしてしまうことが最も効果的である。例えば今まで社会や戦略の問題を考えるに際して、それらの問題が20個の要素で構成されると想定していたのだが、もっと他の要素も考慮の対象に含めることで、それを40個や60個に増やして考えるのである。
現実にも、例えば一個の専門分野の枠内だけでは問題が解決できなくなって、複数の分野に視野を広げる必要性が生じたときに、そういうことが要求される。つまりこの場合、一個の分野だけだとその構成要素は20個なのだが、ここで他の２つほどの分野を同時に視野に入れる必要が生じ、それらの構成要素がやはり同数の各20個だったとすると、それら３つを同時に視野に入れた時には、構成要素の数は合計60個に増えることになる。
ところがこの場合には、人工知能側が先ほどのAパターンのまま規模を拡大して答えを求めようとすると、必要な手間が幾何級数的に激増してしまう。
それに対して人間の直観力が先ほどのようにBのパターン、つまり上三角型に直して扱う能力を持っていて、その能力がこの問題拡大の局面でそのまま使えた場合、その際の演算の手間はせいぜい算術級数的な増大で収まることになる。（またBのパターンのメリットとして、大まかな結果だけは頂点部分のいくつかだけで求めてしまうこともできる）。
つまり人工知能がAのパターンでしか問題を扱うことしかできないのに対し、人間の直観力がBのパターンで問題を扱う能力をもっていた場合、この措置は人間側に非常に有利に作用し、それによって人工知能を引き離してしまうことができる、というわけである。
全体論的アプローチの必要性
ただし今の話では一つ注意すべきことがあり、それは人間がそのように問題を拡大して３つの分野を視野に入れるという場合、今も世の中で普通によく行われているように、それらの３つの分野を、その各分野だけしか知らない３人の専門家にそれぞれ別々に分担させて、最後に各自が持ち寄った答えを合計する、というのでは駄目だということである。
それがなぜ駄目かは、近代の歴史で国家戦略を立案する際などに実際に吹き出てしまっていた。その際には軍事しか知らない専門家が出した解答と、経済しか知らない専門家が出した解答は全く違ったもので、それを混ぜ合わせてもしばしば最悪の折衷策にしかならなかったのである。こういう場合、全部の分野を視野に入れた者が一人は存在して、その１個の頭脳が立案した戦略だけが有効で、それはばらばらな専門家を何人集めても絶対に生まれてこないものなのである。
これに似たことは、例えば３つの分野が、内部にそれぞれ先ほどの状況証拠「６」のような「神の宿る細部」を抱えている場合にも起こり、むしろその話の方がわかりやすいかもしれない。つまり次の左図のように、もし問題のその部分をいじると、それをいじった影響が３つの分野を回る格好で大きくつながって状況を巨視的に変えてしまうが、分野１個の中だけではそれらがつながらないので、巨視的な変化が起こらないとすればどうだろう。
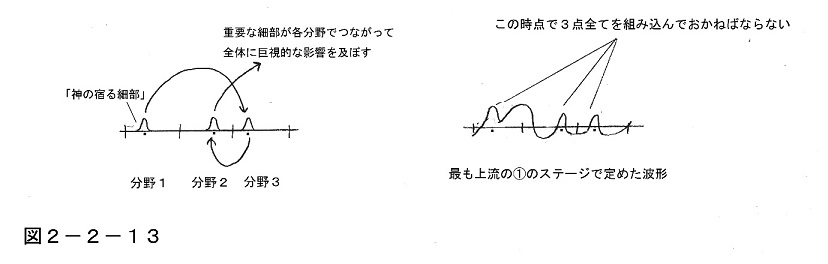こういう問題では、一番上流のステージで波形パターンを設定する際に、右図のように３つの分野全体にまたがる形で、それら３点を最優先でそこに組み込んでおかねばならない。
ところがそのためには、最初の時点で３つの分野全体を視野に収めて、その重要ポイントを全部ピックアップできる人間が存在していることが必要である。それを行っておくことで、初めて状況証拠「５」のような形が実現できるのだが、１つの分野の中だけで考えていると、そもそもそこが重要ポイントであるということ自体がわからないのである。
一方人工知能の場合はどうかというと、当然のことだが直観力をもたない人工知能は、前もってその特殊な３点を知ることができない。むしろその存在は、答えが完全にわかった後でようやくその結果から知ることができる性質のものなので、とにかく60個全部をまとめて力技で扱うしか方法がなく、そうなると、先ほどの数学的なメカニズムがもろに効いてきてしまうのである。
逆に人間側もそれができる者が一人は存在していることが条件なのだが、そういう人間の頭の中では、この能力を使ってさらに手間を簡略化できる。こういう場合、たとえ構成要素の数は60個でも、実際にそれらの特殊な３点と関わりをもって、全体を回る影響に参加しているのはその一部だけで、残りの要素は当面除外しても大枠にはそれほど影響しないことがある。ところがこの能力を使えばしばしばその両者を判別できるのである。
その際には一番上流のステージでは、60個のうちのせいぜい1/3ぐらいだけを考慮してそれで大枠を決めることができ、残りの40個ほどの要素は後回しにして下流の２番目、３番目のステージで初めて扱う格好にしても十分に間に合う。
そうなればその人間は、たとえ問題を拡大して要素を60個に増やした場合でも、頭の中での手間数自体は、構成要素20個で考えていた時と大して変わらないことになり、少なくとも量的な面に関する限り、手間や負担はさほど拡大しないことになるわけである。
参考・なお参考までに述べておくと、この「ばらばらな分野の答えを集めても真の解答にはならない」ということは、作用マトリックスを使えば、もっと根本的なレベルから数学的に示すことができる、というよりそもそもこの話は実はこのツールから導かれる最大の結論である。興味のある読者は「物理数学の直観的方法」を参照していただきたいが、同書をお読みでない読者のためにここでも一言だけその概要を述べておこう。
それは簡単に言えば、一般に行列演算では内部を小行列に分割して、それを各個にＮ乗したものと、全体をＮ乗したものは通常は一致しないからである。
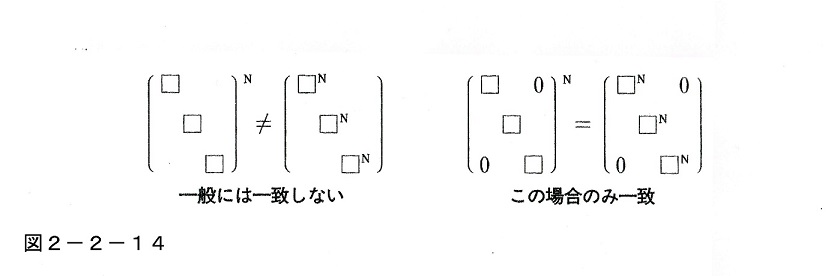
この場合、右辺のように分割して各個にＮ乗したものが、ばらばらな専門家の結論を単純に集めたもので、左辺のように全体をＮ乗したものが、全体論的に１個の頭脳で導かれた結論である。
ただし両者が例外的に一致する場合があり、それは図の右のように行列内部で残りの部分が０、つまり各分野の相互作用が完全にゼロだった場合である。しかしそうでない一般の場合には左図のように両者は一致せず、答えそのものが違ってきてしまうのである。
常識とは少し違っていた人間側の「集団智」
それはともかく、その話を念頭に先ほどのディラックの例を振り返り、そこでは何人もの後継者との間で上流から下流へ向かう構図が共有されて、全体としてディラックを頂点とする一つの大きなピラミッド（あるいは上三角型のBパターン）が構成されていた、という話に注目すると、そこには今までと違う形で人間の「集団智」の可能性が示されているようである。
というよりそもそもわれわれは「集団智」というもののあり方を何か勘違いしていたらしく思われるのであり、今までは先ほどのように、単分野だけの専門家を大勢集めることで、そうした集団智が発揮できると考えてきた。しかし上で見たようにそれは例外的なケースを除けば有効ではなく、むしろ一般の場合には、複数の人間の間でインスピレーションが上流から下流にバトンのように受け渡されてBのパターンを構成してこそ、真の意味での「集団智」を発揮できるのである。
そしてそれが実現された場合には一種の副産物も得ることができ、今まで人間側が人工知能との対決でどうしても不利を強いられていたポイントが一つカバーされうることにもつながる。その弱点とは、人工知能側がメモリー増設などでいくらでも頭脳の規模を拡大していけるのに対し、人間側は一個一個の頭脳サイズは生まれながらに定められてしまって、脳の本来の容量以上にそれを増やすことができない、という不利を抱えていたことである。
ところがもし上のような形で、複数の人間の間で大きな上三角型のBパターンを作れるならば、その時に人間側が持っているメモリーの総量は全員の合計分である。つまり実質的にメモリー容量が人数分だけ増すことになり、頭脳の量的拡大が可能になると解釈することができるわけである。
そうなればその面での人間側のハンディが取り払われることになる一方、人工知能側はインスピレーションの共有ができないので、このメカニズムに割り込んで途中に介在することはできない。かといって人工知能同士でこれと同じものを作ろうとしても、それぞれの個体がどれも全く同じなので、こういう序列をもった関係を構成すること自体に最初から意味がない。つまりもしそうしたものも考えてよいということになると、人間側の潜在力は遥かに大きなものとして捉え直すことが可能になるわけである。
全体論的な直観力の威力
それはともかく、もしそのように人間側が問題の拡大で人工知能を引き離そうとする場合、具体的にその威力はどのぐらいのものになるだろうか。それをやってみると、驚くほどの威力をもっていることがわかるのである。
そこで早速、先ほどの「３つの分野を同時に扱って構成要素を20個から60個に増やす」という話の場合に、それがどのぐらいになるかを見てみよう。（もっともその話で想定した「各分野の要素個数が20個」という数字は、作曲などの場合を考えるとやや小さすぎるように思えるが、ここではあえてそういう小さな数字のままで試算しておくことにする）。
こういう場合の手間数がどうなるかというと、それは第１部でも述べたように、演算の手間数は大まかに言って20ｎ回から60ｎ回に拡大することになる。
この場合のｎの値は、要するに作用マトリックスをｎ回かければｎ日後の状態がわかる、ということを意味するのだから、ここではむしろ「問題を何日先まで追っていけば一応の見通しがつくか」の目安と考え、要素個数の増減の話とは一応別の標準値として、共通の数字にしておいた方がよい。そして最初の時点での話を基準に「問題を20日ほど追跡すれば一応の見通しがつく」と考えて、これもやはりとりあえず「20」というやや小さめの値に設定しておこう。
そのように設定してしまえばそこから先は一直線で、要するにこの場合の最終的な結論として、問題を拡大する前の時点では2020回の演算が必要だったが、拡大後に要求される演算は6020回に増大するわけである。
これがどれぐらいの数字かというと、後者の数字は6020＝2020×320と書くこともできるのだから、拡大前と拡大後で何倍ぐらい大きくなっているかの比較では、2020回だったものが2020×320回に増える格好になり、要するに後者は前者の320倍ということになるわけである。
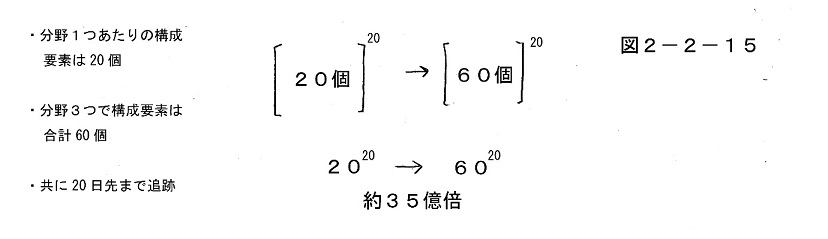
「320倍」と言われてもぴんと来ないと思われるが、これを普通の十進法の数字に書き下すと、実に34.9億倍という数字である。つまり最初からこのようにかなり小さな値に設定しておいた場合でさえも、これだけの数字になってしまうのである。
人間側に秘められていた可能性
これは驚くほど大きな値であり、読者の中にはここで、人工知能との対決に関する今までの常識的な感覚が大きく揺らいでくるのを覚えた方もあると思う。
大体われわれが日ごろコンピューターや人工知能の開発や進歩の話題に接していると、「将来その演算能力が現在の1億倍に向上する」などという話をよく耳にするが、それを聞くともう人間は何をどうやっても太刀打ちできない、という無力感を感じることが多かったのではないだろうか。
ところが上の話を眺めると、そんな無力感が馬鹿馬鹿しく思えた方もあったかもしれない。つまりたとえ人工知能側の演算能力が１億倍に向上したとしても、人間側がそのように３つの分野を同時に頭に入れて全体論的に扱う形で、優れた直観力に物を言わせた場合、その能力は35億倍に匹敵するものとなって、人工知能のたかだか１億倍を一桁上回る格好であっさりと引き離してしまうことができるのである。
もっとも現実の問題として考えると、それを行うことは人間にとってもそれほど容易というわけではない。この場合には先ほど見たように、一番上流にある頭脳が最も鍵を握ることになるが、そもそも今の話で能力拡大を行う前の「１個の分野だけを頭に入れている状態」は、当然ながら人間側のトップクラスの人材を指しており、普通はその能力を身に着けるだけで個人の一生分の努力が限界に達しているものである。
そのため３つの分野についてそれと同様のことを行うというのは、もはや到底不可能と考えられて近代以降、そういう人物は姿を消してしまった。ただそれは一つには近代が先ほどの専門主義に関する錯覚によって、そういう人材は不要であると錯覚し、最初からそういう全体論的な人材を育てることを行ってこなかったことも影響している。
そのため本当にそれができるのかはまだわからず、人間側はこれからそうした人材を輩出するという高いハードルに挑まねばならないのだが、もし将来それができるとすれば、人工知能がせいぜい能力を１億倍に拡大させている間に、人間側は実質的にそれを一桁上回る数十億倍の能力で突き放すことができるかもしれないのである。
そしてこれは単なる量的な意義に留まらない。最近の世の中の常識的な感覚として、将来人工知能が無限に発達した世界では、もう人間は内面の感情的な情緒など、人工知能がわかるはずのない世界に逃げ込むしかなく、その外に出て文明や世界史そのものの行方を左右する重大問題を主役の立場で扱うことは断念するしかないという、逃げの姿勢にとりつかれているように思う。
しかしそんな場所で勝ったところで所詮は自己満足に過ぎず、やはり外の世界で文明や世界史の行方を変えられるような決定的な部分で頂点に立つのでない限り、勝ったことにもならないし、結局は人間の尊厳なども守れないのである。
ところが上の結論はその常識を根底から覆す可能性をもっており、むしろ外的世界でも文明や歴史を左右する最も重要な知的課題に限っては、たとえ人工知能が無限に発達した未来でも、人間側の代表が人工知能では到底及べない能力をもつ存在として、最後まで優位に立ってその頂点のポジションを維持し続ける、という可能性が浮かび上がってくるのである。
そのことが単なる情緒論ではなく、きちんとした数学論理をバックに導かれてくるという事実は、そのような敗北感を払拭して、未来の姿を大きく変えることにつながってくると思われるのである。